| Grand Prix Racing - | The Science of Fast Pinewood Cars |
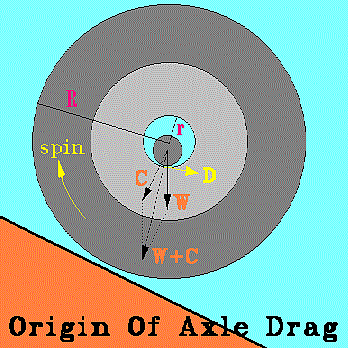
Axles connect wheels to the car body. The system of equations that determines the behavior of the wheels by themselves must be joined to that describing the fall of the body. The wheels levitate the body and so keep it from falling down to the track. This antigravity action allows the body to ride above the track without sliding. But axles exact a price.
Raced by themselves, the wheels roll down the track more slowly than they do when mounted on the car! The weight of the car pushing through its axles power the wheels forward on the ramp. But that same weight focused at each axle pushes down on each wheel creating friction, axle friction .
A model for a grand Prix race is constructed below including wheel inertia and axle and tread drag. Expressions for important dynamic quantities are derived including the total race time.

| E | Energy |
| Ft | Force along the ramp surface |
| m | Mass |
| g | Acceleration by gravity |
| Lr | Length of ramp surface |
| Lf | Length of flat surface |
| y | Distance from starting line or the beginning of the flat |
| O | 'Theta', angle the ramp forms with horizon |
| t | Time from starting line or the beginning of the flat |
| a | Acceleration of the car |
| v | Speed of the car |
| v0 | Speed of the car at the bottom of the ramp |
| I | Moment of inertia of a wheel |
| R | Outer radius of a wheel |
| r | Inner radius of a wheel |
| n | Axle friction coefficient |
| u | Tread drag coefficient |
| Dr | Composite drag on the ramp |
| Df | Composite drag on the flat |
| tc | Coasting time, how long it takes the car to stop |
| yc | Coasting distance, how far the car goes before stopping |
Important expressions derived for this model include:
| Composite drag on flat | Df = nfFfrf/Rf + 2uf(Ff/2+wf) + nrFrrr/Rr + 2ur(Fr/2+wr) |
| Composite drag on ramp | Dr = DfcosO |
| Inertial mass | M = m + 2If/Rf2 + 2Ir/Rr2 |
| Energy Relation on ramp | E = -mgLsinO = -mg(L-y)sinO + Mv2/2 + Dry |
| Equations of Motion on ramp | Ft = ma = (m/M)(-mgsinO-Dr) |
| Time on ramp | t(y) = \[2yM/(-mgsinO-Dr)] |
| Speed on ramp | v(t) = t(-mgsinO-Dr)/M |
| Position on ramp | y(t) = t2(-mgsinO-Dr)/2M |
| Initial speed on flat | v0 = \[2Lr(-mgsinO-Dr)/M]cosO |
| Energy Relation on flat | E = Mv02/2 = Mv2/2 + Dfy |
| Equations of Motion on flat | Ft = ma = - 2Ifa/Rf2 - 2Ira/Rr2 - Df |
| Coasting time | tc = \[2ycM/Df] |
| Coasting distance | yc = Mv02/2Df |
| Speed on flat | v(t) = (tc-t)Df/M |
| Position on flat | y(t) = v0t - t2Df/2M |
| Total time | t = \[2M/Df] ( Lr/\[yc] + \[yc] - \[yc-Lf] ) |
This model of a Grand Prix race includes a car with wheels and axles but no air resistance. Analysis is split between a starting ramp section and a flat coasting section.
In an attempt to be as general as possible, all of the car model parameters are represented. For most Grand Prix cars, some of these parameters will be of little effect individually. For example, Ff and Fr can be specified separately. But in the most frequent case, nf = nr, Rf = Rr and rf = rr, so the axle drag only depends on the total Ff + Fr, without giving different results for different distributions. But this is only true on a ramp or flat surface.
Since there are two wheels in the front and two in back, only half the axle force will be felt by each tire of the pair. But since the expression of work done by axle friction is the same for each wheel of the pair, we can multiply by two instead of writing a separate term for each wheel.
Something similar happens in the wheel kinetic energy terms. In that case, the 1/2 is in the energy relation and the 2 is the number of wheels on the front or back of the car.
________Potential______ + _Kinetic Energy_ + _________Work By Drag__________
Track Car Car Wheels Axles Tread
E = -mgLsinO = -mg(L-y)sinO + mv2/2 + Ifv2/Rf2 + (nfFfrf/Rf + 2uf(Ff/2+wf))ycosO
+ Irv2/Rr2 + (nrFrrr/Rr + 2ur(Fr/2+wr))ycosO
A few definitions will tame this energy relation and make its terms more meaningful.
M, the inertial mass of the car is,
M = m + 2If/Rf2 + 2Ir/Rr2 and
Df, the mechanical drag on a flat track is defined with Ff and Fr evaluated at O=0,
Df = nfFfrf/Rf + 2uf(Ff/2+wf) + nrFrrr/Rr + 2ur(Fr/2+wr)
There is no centrifugal force on the ramp, so keep in mind that
Ff + Fr = 5 oz - 2wf - 2wr, where 5 oz is the AWANA weight limit.
That makes the mechanical drag on the ramp, Dr, less than Df on the flat by a factor of cosO because the normal force is reduced by cosO.
Dr = DfcosO
The complete energy relation can now be written as,
E = -mgLsinO = -mg(L-y)sinO + Mv2/2 + Dry
Group terms in sinO and v2 to reduce to an equivalence between potential energy and kinetic energy plus the work of energy drain due to drag:
-mgysinO = Mv2/2 + Dry
Solve for velocity, v, in terms of position, y:
v(y) = \[2y(-mgsinO-Dr)/M]
To get time in terms of position, separate variables in position, y, and time, t, and integrate:
/ y / t
| dy/\[y] = \[2(-mgsinO-Dr)/M] | dt
/ 0 / 0
/ y
| dy/\[y] = [2\[y]](0,y) = 2\[y] - 0 and
/ 0
/ t
\[2(-mgsinO-Dr)/M] | dt = [\[2(-mgsinO-Dr)/M]t](0,t) = \[2(-mgsinO-Dr)/M]t - 0
/ 0
So, 2\[y] = \[2(-mgsinO-Dr)/M]t
Solve for time, t, in terms of position, y:
t(y) = \[2yM/(-mgsinO-Dr)]
Solve for position, y, in terms of time, t:
y(t) = t2(-mgsinO-Dr)/2M
Solve for speed, v, in terms of time, t, by taking the derivative of position, y(t) w.r.t. (with respect to) small changes in time, t:
v(t) = d(y(t))/dt = d(t2(-mgsinO-Dr)/2M)/dt
Since m, g, O, D1 and M do not change as time progresses,
v(t) = (dt2/dt)(-mgsinO-Dr)/2M)
The derivative of t2 w.r.t. t, dt2/dt is 2t. Substituting and simplifying give:
v(t) = t(-mgsinO-Dr)/M
Solve for acceleration in terms of t, by taking the derivative of v(t) w.r.t. t.
a(t) = d(v(t))/dt = d(t(-mgsinO-Dr)/M)/dt
Again, all parameters are constant, except time itself. The derivative of t, dt/dt is 1 (one). Substituting gives:
a(t) = (-mgsinO-Dr)/M
So the constant acceleration is the tangental weight force reduced by the axle drag over inertial mass.
A force equation can be written in terms of the inertial mass:
Ma(t) = (-mgsinO-Dr)
By subtracting the force of wheel spin, 2Ifa/Rf2 + 2Ira/Rr2, from both sides, the equation of motion along the ramp is revealed:
F = ma = -mgsinO - 2Ifa/Rf2 - 2Ira/Rr2 - Dr
Equivalently, we could have multiplied the acceleration through by the car mass, m, to get:
F = ma = (m/M)(-mgsinO-Dr) Another expression of the same equation of motion.
The equation of motion for a block with no wheels was essentially,
F = ma = -mgsinO - D, where D was nNcosO.
Having wheels has reduced the forces by m/M!
What is the speed at the bottom of the ramp?
t(Lr) = \[2LrM/(-mgsinO-Dr)]
v0 = v(t(Lr)) = t(Lr)(-mgsinO-Dr)/M
v0 = \[2Lr(-mgsinO-Dr)/M]
What is the time at the bottom of the ramp in terms of the speed at the end, v0? Start with t(Lr) from above:
t(Lr) = \[2LrM/(-mgsinO-Dr)]
Factor out 2Lr, leaving a 1/2Lr in the square root to compensate,
t(Lr) = 2Lr\[M/2Lr(-mgsinO-Dr)]
Substitute 1/v0 for the square root.
t(Lr) = 2Lr/v0
Solve for another expression of v0:
v0 = 2Lr/t(Lr)
The energy relation on the flat is similar to that of the ramp. It has many of the same energy terms. But it differs from the ramp in two important ways.
First, the left hand side of the relation presents the amount of kinetic energy initially available on the flat. This amount is the same as the constant E = -mgLsinO on the ramp minus the amount used up in the work of friction.
Second, because this part of the track is flat, theta is zero, O = 0, so sinO = 0 and cosO = 1. There is no potential energy to be considered on the flat. There is only kinetic energy and friction to deal with.
Using the index "0" for the initial velocity, v0, which should really be v0cosO, and the constant Ef for the energy on the flat, the energy relation on the flat is:
Init Kinetic Energy_ = _Kinetic Energy_ + _______Work By Drag_______
Car Wheels Car Wheels Axles wheels
Ef = mv02/2 + Ifv02/Rf2 = mv2/2 + Ifv2/Rf2 + (nfFfrf/Rf + 2uf(Ff/2+wf))y
+ Irv02/Rr2 + Irv2/Rr2 + (nrFrrr/Rr + 2ur(Fr/2+wr))y
The complete energy relation can now be written with M and D as,
E = Mv02/2 = Mv2/2 + Dy
Solve for speed, v, in terms of position, y:
v(y) = \[v02 - 2yD/M]
As a check find speed at y=0, v(0) = v0 as it should.
For what value of position, yc, will speed, v(y), be zero?
0 = \[v02 - 2ycD/M]
Square both sides. Add the negative term to both sides.
v02 = 2ycD/M
Solve for yc, the distance the car coasts before stopping:
yc = Mv02/2D
Rewrite v(y) in terms of the coasting distance, yc, by substituting 2yD/M for v02 and simplifying.
v(y) = \[2(yc-y)D/M]
To get time in terms of position, separate variables in position, y, and time, t, and integrate:
/ y / t
| dy/\[yc-y] = \[2(D/M)] | dt
/ 0 / 0
/ y
| dy/\[yc-y] = -2\[yc-y](0,y) = -2\[yc-y] + 2\[yc-0]
/ 0
/ t
\[2(D/M)] | dt = [\[2(D/M)]t](0,t) = \[2(D/M)]t - 0
/ 0
So \[2(D/M)]t = 2\[yc] - 2\[yc-y]
t(y) = \[2ycM/D] - \[2(yc-y)M/D]
Checking y = 0 gives, t(0) = \[2ycM/D] - \[2ycM/D] = 0.
What is the time it takes for the car to coast to a stop, tc? Set y to yc:
tc = t(yc) = \[2ycM/D] - \[2(yc-yc)M/D] = \[2ycM/D]
Rewrite t(y) using this coasting time, tc:
t(y) = tc - \[2(yc-y)M/D]
Solve for the position, y, in terms of time, t; rearrange the expression for t(y):
\[2(yc-y)M/D] = tc - t
Square both sides and clear the multipliers:
yc - y = (tc-t)2D/2M
Subtract the coasting distance, yc, and multiply both sides by -1:
y(t) = yc - (tc-t)2D/2M
By substituting the expressions for yc and tc in v0 back into this expression we can get an alternate form that mimics the classic ballistic expression for position:
y(t) = v0t - t2D/2M
We can now find velocity in terms of time, v(t):
v(t) = v(y(t)) = \[2(yc - yc + (tc-t)2D/2M)D/M]
Simplifying:
v(t) = (tc-t)D/M
Note that at t = 0, v(0) = v0 = tcD/M.
Differentiate velocity, v(t), by time, t, to get the acceleration, a:
a = dv(t)/dt = d((tc-t)D/M)/dt = -D/M
A force equation can be written:
F = Ma = -D
Finally, using the definition of M, the equation of motion along the flat is:
F = ma = - 2Ifa/Rf2 - 2Ira/Rr2 - D
The total time, t, for the race is the time on the ramp plus the time on the flat.
t = 2Lr/v0 + tc - \[2(yc-Lf)M/D]
Use v0 = \[2Dyc/M] and tc = \[2ycM/D] in terms of yc to get:
t = Lr\[2M/Dyc] + \[2ycM/D] - \[2(yc-Lf)M/D]
Factor out \[2M/D]:
t = \[2M/D] ( Lr/\[yc] + \[yc] - \[yc-Lf] )
Each of these terms speaks volumes about the race without air resistance! Note the only non-constant parameter is the coasting distance. The coasting distance of your can be considered its figure of merit. Now, yc = Mv02/2D, your car's linear kinetic energy divided by its mechanical drag force. Substituting this expression for coasting distance and simplifying begins to shine some light on the term's meanings.
t = M/D ( 2LrD/Mv0 + v0 - v0\[1-2LfD/Mv02] )
Let's write these terms in words:
time = inverse drag acceleration ( twice drag work divided by momentum on ramp plus speed at end of ramp reduced by drag work divided by linear kinetic energy on flat )
This is just the start of an analysis that summarizes much of the physics of the race.
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |