| Grand Prix Racing - | The Science of Fast Pinewood Cars |
In this model, a simple form of kinetic (moving) friction is added. It is a kind of friction that shows up when a block slides on a ramp. To make this model more like the Grand Prix race, a flat runout is added at the end of the ramp. Technically, we should make the center of the block a part of the model, but to keep it simple, we won't. The flat allows some "new" behavior to be considered: coasting to a stop.
Children love slides. Remember how you zoomed along and landed in the sand? Sometimes your shoes would catch on the side and jolt you to a stop, or your sweaty legs would stick and slow you to a crawl. Did you ever sprinkle sand on a slide? If you did, you found a way to cool the slide and go faster!

| E | Energy |
| Ft | Force along the ramp surface |
| m | Mass |
| g | Acceleration by gravity |
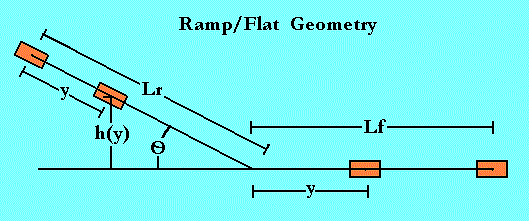
| Lr | Length of ramp surface |
| Lf | Length of flat surface |
| y | Distance measured from the start of the ramp or flat |
| O | 'Theta', angle the ramp forms with horizon |
| n | Sliding friction coefficient |
| t | Time from starting line or the beginning of the flat |
| a | Acceleration of the sliding car |
| v | Speed of the sliding car |
| v0 | Speed of the sliding car at the bottom of the ramp |
| tc | Coasting time, how long it takes the car to slide to a stop |
| yc | Coasting distance, how far the car slides to a stop |
Important expressions derived for this model include:
| Energy Relation on ramp | E = -mgLsinO = -mg(L-y)sinO + mv2/2 + nmgycosO |
| Equations of Motion on ramp | Ft = m a = mgsinO + nmgcosO |
| Time on ramp | t(y) = \[2y/g(-sinO-ncosO)] |
| Speed on ramp | v(t) = g(-sinO-ncosO)t |
| Position on ramp | y(t) = g(-sinO-ncosO)t2/2 |
| Initial flat speed | v0 = \[2gLr(-sinO-ncosO)]cosO |
| Energy Relation on flat | E = mv02/2 = mv2/2 + nmgy |
| Equations of Motion on flat | Ft = m a = -nmg |
| Coasting time | tc = v0/ng |
| Coasting distance | yc = v02/2ng |
| Time on flat | t(y) = (\[yc] - \[yc-2y])/\[ng] |
| Speed on flat | v(t) = v0 - ngt |
| Position on flat | y(t) = v0t - ngt2/2 |
| Total Time | t = (\[2Lr2/yc] + \[yc] - \[yc-2Lf])/\[ng] |
The work done by sliding friction against a block on the ramp is the force, F, times the distance traveled, y. This force is the force pushing down at right angles to the slide surface, the normal force, N, times a sliding friction coefficient, n. The normal force, N, is the weight of the block, mg, times the cosine of the ramp angle, O, since the ramp supports that part of the weight. Substituting a step at a time,
work = Fy = nNy = nmgycosO
Now the energy relation can be written with this new work term,
Conservation of Energy
_______Potential_______ + Kinetic Energy + Work done by Friction
Track Car Car
E = -mgLsinO = -mg(L-y)sinO + mv2/2 + nmgycosO
Group terms in weight, mg, and velocity squared, v2,
mgy(-sinO-ncosO) = mv2/2
Solve for speed, v, in terms of position, y,
v(y) = \[2gy(-sinO-ncosO)]
Separate variables in position, y, and time, t, and integrate,
/ y / t
| dy/\[y] = \[2g(-sinO-ncosO)] | dt
/ 0 / 0
/ y
| dy/\[y] = 2\[y]
/ 0
/ t
\[2g(-sinO-ncosO)] | dt = \[2g(-sinO-ncosO)]t
/ 0
Together these results yeild:
2\[y] = \[2g(-sinO-ncosO)]t
Solve for time, t, in terms of position, y,
t(y) = \[2y/g(-sinO-ncosO)]
Solve for position, y, in terms of time, t,
y(t) = g(-sinO-ncosO)t2/2
Solve for speed in terms of time, t, by taking the derivative of position in terms of time, y(t) w.r.t. t,
v(t) = g(-sinO-ncosO)t
Solve for acceleration in terms of time, t, by taking the derivative of speed, v(t), w.r.t. t,
a(t) = g(-sinO-ncosO)
Use this acceleration to write the equation of motion along the ramp:
Ft = m a = mgsinO + nmgcosO (tangental)
And write the normal to the ramp as a result of Newton's Third Law:
Fn = m a = mgcosO - mgcosO = 0 (normal)
At the bottom of the ramp, the car transitions to the flat. It's potential energy has been converted into kinetic energy on the ramp. So the sliding car body begins its journey on the flat with this motion energy, mv02/2. v0 is the inital speed. It is found by using the ramp length for y in the ramp expression for v(y).
v0 = \[2gLr(-sinO-ncosO)]
But instead of using this expression for v0, it should really be v0cosO. That is, it should be reduced by cosO since some energy is lost at the abrupt join. So,
v0 = \[2gLr(-sinO-ncosO)]cosO
Suppose a block was given an initial speed on a horizontal surface. How far would it travel before it stopped? How long would it take it? Though we could write the energy relation, we will begin with the equations of motion along the ramp. The equations of motion along the flat are easily obtained from the equations of motion on the ramp by setting O, the ramp angle, to zero.
Ft = m a = -nmg (tangental)
Fn = m a = mg - mg = 0 (normal)
Solve for the acceleration from the tangental equation, Ft:
a = -ng
Since a = dv/dt, integrate using the initial velocity, v0, and the final velocticy, v, which is smaller, to get,
/ v / t | dv = -ng | dt / v0 / 0
The result is,
v-v0 = -ngt
Solve for the speed in terms of time, t,
v(t) = v0-ngt
Solve for the time it takes to come to a stop, v = 0; coasting time, tc,
tc = v0/ng
Since v = dy/dt, we integrate again, but start measuring position, y, along the flat at zero.
/ y / t / t | dy = v0 | dt - ng | tdt / 0 / 0 / 0
This gives the relationship between position and time:
y(t) = v0t - ngt2/2
But when the time is the coasting time, tc, the distance traveled, yc, is the coasting distance, yc.
yc = v0tc - ngtc2/2
Use tc = v0/ng to get,
yc = v02/ng - v02/2ng = v02/2ng
This last term shows the coasting distance as the ratio between the initial kinetic energy mv02/2 and the force of drag on the block on the flat, nmg.
From y(t) we get t(y). Rewrite in standard polynomial form in terms of t,
ngt2/2 - v0t + y = 0
Now solve the quadradic for t
t(y) = v0/ng +/- \[v02 - 2yng]/ng
Since tc = v0/ng, the plus sign must be an invalid choice since then the car body would have a greater time somewhere on the track before it stopped. Since that doesn't make sense, the negative sign is kept.
t(y) = v0/ng - \[v02 - 2yng]/ng
Notice we can write this in terms of tc or yc,
t(y) = tc - \[tc2 - 2y/ng]
t(y) = (\[yc] - \[yc-2y])/\[ng]
Time spent on the ramp is found by using y = Lr,
tr(Lr) = \[2Lr/g(-sinO-ncosO)]
And time on the flat by using y = Lf.
tf(Lf) = (\[yc] - \[yc-2Lf])/\[ng]
Note that the two y's above have different origins. One at the start of the ramp and the other at the start of the flat.
To express tr(y) in terms of yc, yc need to have v0 expanded.
yc = v02/2ng = gLr(-sinO-ncosO)/ng
Now we can see that tr in terms of yc is
tr(Lr) = \[2Lr2/ycng]
The total time in y and yc is
t = tr(Lr) + tf(Lf) = (\[2Lr2/yc] + \[yc] - \[yc-2Lf])/\[ng]
On the flat the car begins only with kinetic energy, mv02/2.
If all of this energy is consumed by sliding friction, the car will stop on the track. The car will need to do work equal to the force of sliding friction times the length of the flat to make it. But the force of friction is now greater since the inclination angle is zero. It is the car's full weight times the sliding friction coefficient. So the energy relation of the initial energy to the final work done is:
mv02/2 = nmgyc
This relation can be solved for yc to see how far the car can go:
yc = v02/2ng, just as we saw above.
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |