| Grand Prix Racing - | The Science of Fast Pinewood Cars |
Racing from the starting ramp onto the flat of your Grand Prix track is a critical time for your car. It is travelling its fastest and experiencing the most mechanical drag that it will in the race. It is important to model this section reasonably well.
The model developed here is used to show in the simple race trajectory model that ignoring the "real" trajectory at the zero-join is a reasonable way to avoid undue complexity in the simple closed race model. This conclusion is based on two results.
The model presented here is first geometric (trajectory) presented in three parts, then dynamic. However, the dynamics are simplified by not considering friction. For the short time spent on this zero-transition, about 4 hundreths of a second, the comparison is reasonable.
A more detailed approach to the zero transition problem is through solving the equations of motion. The problem is similar to finding the trajectory and dynamics of a ladder sliding down the side of a wall.
Though it is possible to model the dynamics on the three sections of the zero length transition trajectory by three sets of closed equations, it becomes cumbersome at best. The relevance of separately calculating the dynamics on the short transition trajectory is certainly in question. A car spends less than 4 hundreths of a second on this part that is less than the distance between the axles of the car. This article shows that there is no loss in the behavior of the model if the trajectory at the zero length transition is ignored.
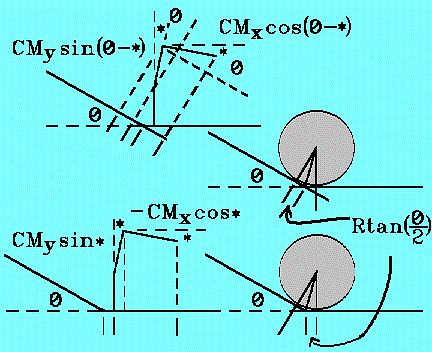
To explore the significance of the transition trajectory in the zero length transition model, break up the trajectory into three parts. In the AWANA track model developed in this manual, the transition section was reduced to zero length for convenience. In general it has a greater length and changes the trajectory. But even in the zero length case, the transition produces a different trajectory arc from the ramp or flat. Trajectory is considered here for the zero length case only.
| The Ramp | L1 = Distance from CM at starting line to CM where car's front wheel touches the flat. |
|---|---|
| The Transition | L2 = Distance from CM where front wheels touch the flat to CM where rear wheels touch it. |
| The Flat | L3 = Distance from CM where rear wheels touch the flat to CM where nose crosses the finish line. |
Since it is no less difficult, we will not only find L3, but L1 and L2 as well. First, we will find an expression for the length of a car's trajectory on the flat, then the ramp and finally the transition. This progression allows us to find the easy length first, then the harder ones. Discussion and derivations of trajectory end points found in the Car Trajectory model will not be repeated here.
First note the previously derived distance to the finish line.
Finish: N + B - CMx and when * is not zero, (N + B - CMx)cos* + CMysin*

On the starting end of the flat, the center of mass is in front of the point where the ramp and flat join. But the rear axle is also a small distance ahead of the join.
How much? The wheel is touching the flat and the ramp at the same instant. These contact points form an isosceles triangle with the axle. The Ramp is tipped at an angle theta, O, a negative number since the ramp slopes down. Because the line through the axle and the contact point on the ramp forms a right angle with the ramp surface, the isosceles triangle must open at an angle equal to theta. This means the small distance that the center of mass is ahead of the join must be Rrtan(O/2).
Now we can see that the center of mass is Rrtan(O/2) plus CMx ahead of the track join,
Join: Rrtan(O/2) + CMx and when * is not zero, Rrtan(O/2) + CMxcos* - CMysin*
The length of the flat is Lf. To get your car's trajectory length on this third part of the trajectory, L3, we simply subtract the distances from the center of mass to the join and the finish,
L3 = Lf - Rrtan(O/2) - CMx - N - B + CMx
or if * is not zero,
L3 = Lf - Rrtan(O/2) - CMxcos* + CMysin* - (N + B - CMx)cos* - CMysin*
At the starting line, the center of mass is behind it. As derived before, this distance is,
Start: N + B - CMx and when * is not zero, (N+B-CMx)cos* + CMysin*
When the front wheel of your car first touches the flat, the center of mass is behind the joining point of the ramp and flat. This distance is computed the same as that from the starting line, except the nose is not in the picture and the front axle would still have to travel Rftan(O/2) to reach the join. So we can write,
Join: B - CMx + Rftan(O/2) and when * is not zero, (B-CMx)cos* + CMysin* + Rftan(O/2)
The length of the ramp is Lr. To get your car's trajectory length on this first part of the trajectory, L1, we simply add the distance from the center of mass to the starting line and subtract the distance from the center of mass to the join,
L1 = Lr + N + B - CMx - B + CMx - Rftan(O/2)
or if * is not zero,
L1 = Lr + (N+B-CMx)cos* + CMysin* - (B-CMx)cos* - CMysin* - Rftan(O/2)
The second part of the trajectory sweeps out a curve as the car crosses the track join. The rear wheels touch the ramp, while the front touch the flat. The height of the center of mass above the track changes from (Rr+CMycos*+CMxsin*)/cosO to Rr+CMycos*+CMxsin* since O is zero on the flat. From the track model, we see the track height changes according to h(y) = H + ysinO. When the front wheels first touch the flat, y on the ramp is Lr - (B-CMx)cos* - CMysin* - Rftan(O/2) following from the ramp/join discussion above. Adding the height of the center of mass above the track to the height of the track above the flat, we get how high the center of mass is above the flat when the front wheels first touch the flat,
Initial CM height = (Rr+CMycos*+CMxsin*)/cosO + (B-CMx)cos*sinO + CMysin*sinO + Rftan(O/2)sinO
Note that H = LrsinO and so it canceled out in simplifying.
The final height of the center of mass above the track when the rear wheel touches the flat is Rr + CMycos* + CMxsin* from the discussion of the flat. No term is added for the track height since it is zero. The difference between the initial height and final height of transition is, dh,
dh = (Rr+CMycos*+CMxsin*)/cosO + (B-CMx)cos*sinO + CMysin*sinO + Rftan(O/2)sinO - Rr - CMycos* - CMxsin*
The horizontal distance traveled by the center of mass in the transition, db, is the join distance from the ramp rotated plus that on the flat. From above,
db = ((B-CMx)cos* + CMysin* + Rftan(O/2))cosO + Rrtan(O/2) + CMxcos* - CMysin*
As it turns out, the path taken by the center of mass is nearly the line of height dy and base dx! So the distance traveled is very close to
L2 = \[db2+dh2] which is less than B, the separation between the axles.
In summary, the trajectory model equations are as follows. Note that many terms in the expressions derived above cancel so they are simpler in the table.
| EXPRESSION | UNITS | DESCRIPTION |
| * = arctan((Rf-Rr)/B) | degrees | Tilt of car due to different size front and rear wheels |
| h(y) = (Rr + CMycos* + CMxsin*)/cosO + H - ysinO | inches | Height of trajectory on ramp |
| L1 = Lr + Ncos* - Rftan(O/2) | inches | Length of car's trajectory on ramp |
| 0 <= y <= L1 | inches | Range of arc parameter along ramp |
| db = ((B-CMx)cos* + CMysin* + Rftan(O/2))cosO + Rrtan(O/2) + CMxcos* - CMysin* | inches | Base distance of transition |
| dh = (Rr+CMycos*+CMxsin*)/cosO + (B-CMx)cos*sinO + CMysin*sinO + Rftan(O/2)sinO - Rr - CMycos* - CMxsin* | inches | Height of transition |
| L2 = \[dx2+dy2] | inches | Length of car's trajectory on transition |
| 0 <= y <= L2 | inches | Range of arc parameter along transition |
| h(y) = Rr + CMycos* + CMxsin* | inches | Height of trajectory on flat |
| L3 = Lf - (N+B)cos* - Rrtan(O/2) | inches | Length of car's trajectory on flat |
| 0 <= y <= L3 | inches | Range of arc parameter along flat |
Geometry is the scaffold of physics until you look too deep, then it becomes physics. However, in this simplified model, the geometry is in a sense "broken". There is a mathematical discontinuity at the intersection of the ramp and flat trajectories. It is as if we are looking at the traces of particles in the analysis chamber of a particle accelerator. We see the incoming track and outgoing track of the accelerated particle but not a hint of the target particle that caused the deviation in the trajectory.
A simple analysis helps. Write vi and vf for the initial and final velocities of the accelerated particle, your car! Also write vn for the velocity of an imaginary particle that has the same mass as your car. We will assume that vn has a direction that is at right angles to vf. Then we can write the following conservation relations.
mvi = mvf + mvn, conservation of momentum (thinking of the velocities as vectors)
mvi2/2 = mvf2/2 + mvn2/2, conservation of energy (thinking of the velocities as scalars)
then vi2 = vf2 + vn2 so that
vf = vicosO and vn = visinO is a possible solution.
The conservation of energy expression indicates that mvn2/2 amount of energy is lost in the collision to the imaginary particle with speed vn and mass m. But the imaginary particle is not so imaginary, it's the track! Since it has a much larger mass, it won't end up with speed vn, or any speed for that matter. But the energy is absorbed in sound, "CLUNK", heat and small vibrations along the track.
When your car starts out, it has a total energy of mgH. For a typical Grand Prix car on the Official AWANA track (mgH is roughly 200 ozin), the energy loss is about one tenth of that total!
vi is the speed that the car has at the end of the ramp. Then v0, the initial speed on the flat is vicosO. Think about what would happen if O was -pi/2 (-90 degrees). If the car could absorb some of the shock by a bumper or by disintegrating, it would splat on the flat and stay there. Otherwise it would bounce elastically until it came to rest on the flat not far from the "ramp". As O is increased toward zero slightly, the car would seem stunned but manage a bit of speed perhaps bouncing toward the finish line. Further increases in O show faster and faster speeds and smaller bounces until normal values of O are used. Then it is difficult to tell that the speed is decreased. But this analysis assures us that it does.
For the Official AWANA track, cosO is about 0.93. So the car loses about 7% of its speed whether the collision is inelastic, elastic or somewhere in between.
From the change in the momentum of the car (mvi-mvf) and the time it takes the car to pass over the discontinuity (dt), the average force of the collision can be found. When there is a change in momentum, a reaction to something, Newton's third law tells us a force from the opposite direction did it. This is written in this case as,
mvi-mvf = Fdt
Then solving for the force, F,
F = (mvi-mvf)/dt
For a typical Grand Prix car on the Official AWANA track, this force is about 3.5 ounces.
| v0 = vicosO | Initial speed on the flat |
| F = (mvi-mvf)/dt | Average force on track during the transition |
| dE = mvi2sin2O/2 | Energy lost during the transition |
| [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |