| Grand Prix Racing - | The Science of Fast Pinewood Cars |
Imagine a single wheel rolling down a track. Adding friction between the wheel and the track introduces more complexity in the mathematics and changes the course of derivation a bit. As developed here, the model can be used to answer questions having to do with total time and the effects of rolling friction or things like changing the weight or radius of the wheel.
Because of friction, the wheel rolls to a stop. A flat run out is added to the model to find expressions for stopping. The dynamics (accelerations, speed, position and other interesting physical measurements) are modeled on both the ramp part of the track and the flat part.
In this model the small effect of having a center of mass above the track is considered.

| E | Energy |
| Ft | Force along the ramp |
| m | Mass |
| g | Acceleration by gravity |
| Lr | Length of ramp surface |
| Lf | Length of flat surface for run out |
| y | Distance measured from the top of the ramp surface |
| O | 'Theta', angle the ramp forms with horizon |
| t | Time from starting line |
| a | Acceleration of the wheel |
| v | Speed of the wheel |
| v0 | Speed of the wheel at the bottom of the ramp |
| w | Angular speed of the wheel |
| I | Moment of inertia of the wheel |
| R | Outer radius of the wheel |
| u | Rolling drag coefficient |
| Dr | Tread drag on the ramp |
| Df | Tread drag on the flat |
| M | Inertial mass, the effective mass of a spinning object |
| yc | Coasting distance on the flat measured from the join |
| tc | Coasting time from the join |
Important expressions derived for this model include:
| Inertail Mass | m + I/R2 |
| Ramp Tread Drag | Dr = DfcosO |
| Energy Relation on ramp | E = -mgLrsinO = -mg(Lr-y)sinO + mv2/2 + Iv2/2R2 + Dry |
| Equations of Motion on ramp | Ft = m a = -m2gsinO/M - Dr |
| Time on ramp | t(y) = \[2yM/(-mgsinO-Dr)] |
| Speed on ramp | v(t) = (-mgsinO-Dr)t/M |
| Position on ramp | y(t) = (-mgsinO-Dr)t2/2M |
| Drag on flat | Df = umg |
| Initial speed on flat | v0 = \[2Lr(-mgsinO-Dr)/M]cosO |
| Energy Relation on flat | E = Mv02/2 = Mv2/2 + Dfy |
| Time on flat | t(y) = \[2M/Df](\[yc] - \[yc-y]) |
| Speed on flat | v(t) = v0-Dft/M |
| Position on flat | y(t) = v0t - Dft2/2M |
| Coasting time | tc = v0M/Df |
| Coasting distance | yc = v02M/2Df |
| Tread drag coefficient | u = -LrsinO/(LrcosO+yc) |
| Total time | t = \[2M/Df] ( \[Lr2/yc] + \[yc] - \[(yc-Lf)] ) |
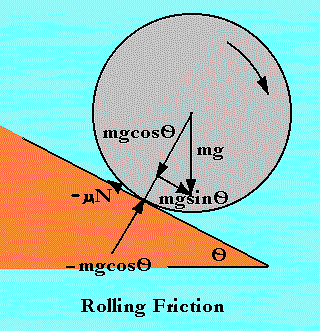
A wheel with radius, R, is rolling down a ramp.
How fast the wheel spins is called its angular speed or rotation rate, w.
Because it is round, the arc distance traveled per unit time, linear speed, is,
v = Rw
The position of the wheel is raised to the center of the wheel instead of being left on the track for simplicity.
h(y) = -(Lr-y)sinO
The energy relation includes the potential energy as well as two terms for the kinetic energy and one for work done by friction. The first term in v is the linear kinetic energy. The second in w is the rotational kinetic energy.
The rolling friction term depends on the normal force (the force through the contact point at right angles to the track surface). Because the normal force changes as the track curves up of down, so does the rolling drag. It is constant on a ramp.
The work or energy expended on the ramp in overcoming friction is
/ y
u | N dy = umgycosO (N=mgcosO, a constant force)
/ 0
Let Df = umg and Dr = DfcosO.
The energy equation is then
E = -mgLrsinO = mgh + mv2/2 + Iw2/2 + Dry
Substitute h(y) for h and v/R for w.
E = -mgLrsinO = -mg(Lr-y)sinO + mv2/2 + Iv2/2R2 + Dry
Let M = m + I/R2, the inertial mass. Now,
E = -mgLrsinO = -mg(Lr-y)sinO + Mv2/2 + Dry
Add the potential and friction to both sides and collect terms in y.
y(-mgsinO-Dr) = Mv2/2
Solve for v2.
v2 = 2y(-mgsinO-Dr)/M
Take the square root.
v(y) = \[2y(-mgsinO-Dr)/M]
v(y) = dy/dt in terms of y, so separate the variables in y and t and integrate to get y(t).
/ y / t
| dy/\[2y(-mgsinO-Dr)/M] = | dt
/ 0 / 0
/ y
The left hand side has the form | dy/\[Ay] which is 2\[Ay]/A
/ 0
for A constant = 2(-mgsinO-Dr)/M, so
/ y
| dy/\[2y(-mgsinO-Dr)/M] = \[2y(-mgsinO-Dr)/M]/(-mgsinO-Dr)/M
/ 0
/ t
| dt = t
/ 0
Put these individual results together again and simplify.
t(y) = \[2yM/(-mgsinO-Dr)]
Square both sides.
t2 = 2yM/(-mgsinO-Dr)
Solve for y.
y(t) = (-mgsinO-Dr)t2/2M
Acceleration in terms of time can be found a couple of ways. First, use the energy relations. Note that the law of conservation of energy requires E to be constant for a conservative force like gravity with the "sinks" like friction, accounted for.
E = -mgLrsinO = -mg(Lr-y)sinO + Mv2/2 + Dry = constant, so
This makes it possible to find the time derivative of each term.
dE/dt = dmgLrsinO/dt = -dmg(Lr-y)sinO/dt + d(Mv2/2)/dt + Drdy/dt
The result is,
dE/dt = 0 = mgsinOdy/dt + Mvdv/dt + Drdy/dt
Then since dy/dt = v and dv/dt = a,
dE/dt = 0 = mgvsinO + Mva + Drv
Subtract the potential and friction on each side.
Mva = -mgvsinO - Drv
Mav = v(-mgsinO-Dr)
Divide out the velocity, v. Solve for a.
a(t) = (-mgsinO-Dr)/M
Another way to get the acceleration and speed in terms of time is to plug y(t) into v(y). The first result is the speed in terms of time. Take the time derivative of this speed and the acceleration in terms of time pops out. Note that -mgsinO, Dr and M are all constant on the ramp. You can carry out this program yourself to check the a(t) expression above.
Continuing, multiply a(t) by mass, m, to get the equation of motion along the ramp.
Ft = m a = m(-mgsinO-Dr)/M
The force in the normal direction cancels, so
Fn = m a = mgcosO - mgcosO = 0
To get the speed at the ramp bottom, use y = Lr in v(y) = \[2y(-mgsinO-Dr)/M]
v(Lr) = v0 = \[2Lr(-mgsinO-Dr)/M]
The wheel starts out on the flat with an initial velocity, v0. But instead of using the expression of v0 above, it should really be v0cosO, that is, reduced by cosO since some energy is lost at the abrupt join. Begin with the energy relation that holds on the flat. The initial energy is that of the wheel at the bottom of the ramp.
E = Mv02/2 = Mv2/2 + Dfy for Df = umg
Note that this expressoin says that the work due to drag on the flat is the difference in the initial energy and the final energy.
Dfy = M(v02-v2)/2
With no external acceleration, the expression can be directly solved for v(y).
v02-v2 = 2Dfy/M
v2 = v02 - 2Dfy/M
v(y) = \[v02 - 2Dfy/M]
/ y / t
| dy/\[v02 - 2Dfy/M] = | dt
/ 0 / 0
/ y
The left hand side has the form | dy/\[k-Ay] which is -2\[k-Ay]/A
/ 0
for A constant = 2Df/M, and k constant = v02 so
/ y
| dy/\[v02 - 2Dfy/M] = -2\[v02 - 2Dfy/M]/2Df/M - (-2\[v02 - 2Df0/M]/2Df/M)
/ 0
/ t
| dt = t
/ 0
Bringing the two sides together and simplifying
t(y) = v0M/Df - \[v02M2/Df2 - 2yM/Df]
Now solve for y(t)
v0M/Df - t = \[v02M2/Df2 - 2yM/Df]
Square both sides and isolate y
y(t) = v02M/2Df - Df(v0M/Df - t)2/2M
Multiply out the square and simplify
y(t) = v0t - Dft2/2M
Plug y(t) in v(y) to get v(t)
v(t) = \[v02 - 2v0tDf/M + t2Df2/M2]
The inside of the square root is a square
v02 - 2v0tDf/M + t2Df2/M2 = (v0 - Dft/M)2 so
v(t) = v0 - Dft/M
A few things can be said about how far and how long the wheel rolls. We can even find the tread friction coefficient, u, just by timing the wheel!
v - v0 = - Dft/M
The wheel stops when it has no speed, v = 0. The time it takes (measured from the bottom of the ramp) is, tc, the coasting time so
-v0 = -tcDf/M
tc = v0M/Df
tc = \[2LrM(-mgsinO-Dr)]/D
The coasting distance is how far it goes in the coasting time. It's the same as the distance from the end of the ramp to where it would stopif the flat were long enough.
yc = y(tc) = v0tc - tc2Df/2M
yc = v02M/Df - Df(v0M/Df)2/2M
yc = v02M/Df - v02M/2Df
yc = v02M/2Df
yc = Lr(-mgsinO-Dr)/Df since v0 = \[2Lr(-mgsinO-Dr)/M]
To get an expression for the tread friction coefficient, start with the expression for the coasting distance and isolate the tread drag, Df.
Df = Lr(-mgsinO-Dr)/yc
Expand Dr to expose the coefficient, u.
umg = mgLr(-sinO-ucosO)/yc
u = -LrsinO/yc-LrucosO/yc
Group terms in u and simplify
u( 1 + LrcosO/yc ) = -LrsinO/yc
u(yc+LrcosO) = -LrsinO
u = -LrsinO/(LrcosO+yc)
This is the height of the ramp divided by the total horizontal distance traveled. For a wheel rolling down a ramp and coasting to a stop, the tread friction coefficient can be computed like the static friction coefficient on a ramp that extends all the way to where the wheel stops rolling.
Using r and f to index the time on the ramp and flat, express time in terms of the coasting distance and distance traveled so far, y.
tr(y) = \[2yM/(-mgsinO-Dr)]
tr(y) = \[2y2M/ycDf]
The last time on the ramp is reached when the wheel gets to the bottom of the ramp, y = Lr.
tr(Lr) = \[2Lr2M/ycDf]
tf(y) = \[2ycM/Df] - \[2ycM/Df - 2yM/Df]
Simplify
tf(y) = \[2M/Df](\[yc] - \[yc-y])
The last time on the flat is reached when the wheel gets to the end of the flat, y = Lf.
tf(Lf) = \[2M/Df](\[yc] - \[yc-Lf])
t = tr(Lr) + tf(Lf) = \[2Lr2M/ycDf] + \[2M/Df](\[yc] - \[yc-Lf])
t = \[2M/Df] ( \[Lr2/yc] + \[yc] - \[(yc-Lf)] )
To get the equations of motion, differentiate the velocity with respect to time.
v(t) = v0 - Dft/M
a(t) = dv/dt = -Df/M
Multiply by mass and we get the equation of motion along the ramp,
F = ma = m(-Df)/M
Had we begun with this, each of the expressions obtained above could have been derived also. It's always a good idea to work through this approach, if possible, to verify the results of the energy approach.
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |