| Grand Prix Racing - | The Science of Fast Pinewood Cars |
Wheels are so very important to your Grand Prix car. They are just as important to a mathematical car model. Their geometry and physical nature must be disected and laid out explicitely. It is one thing to say that wheels are round, but how is it said mathematically? It is something else to say they spin, but what does that mean physically?
Below, a model of the geometry of wheels is developed. The shape of the wheel is a very important factor in how much energy is stored as it spins and how quickly the wheel accelerates. The shape of a wheel is captured here, the dynamics take a couple more sections to develop.

| pi | The ratio of the circumference of a circle to its diameter = 3.141592... |
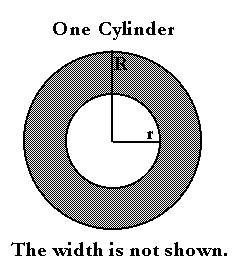
| R | Outer radius of a cylindar |
| r | Inner radius of a cylindar |
| w | Width of a cylindar |
| V | Volume of a cylindar |
Important expressions derived for this model include:
| Volume of a cylindar | V = wpi(R2-r2) |
A wheel looks like a circle, a fat, wide circle. If it were just a circle, we could model the wheel's shape by its center and how far across it measures. Its center would be its position above and along the track. The distance across the circle is its diameter. Half of that distance crosses the wheel's center. This half-diameter is called the circle's radius.
The place where the circle touches the track is its contact point. No matter which part of the circle touches the track, its center is always directly above the point of contact. In fact, the center is lifted up exactly one radius off the track surface.
A wheel described by a simple circle is not much of a wheel. Even if the middle is filled in, making it a disk, it would not look like the wheels of your car. Those wheels are more like "fat" circles, or disks with a small circular hole at the center. But they are also wide, yet not quite like a donut. A donut is solid; your wheels are a hollowed out shell. How can we model our wheels if none of these shapes work?
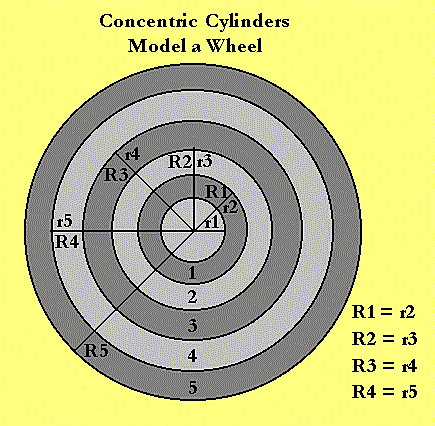
Wheels exhibit a special form of repeated motion called laminar motion. In laminar (literally "layered") motion, particles of matter follow the same path or orbit over and over again. The whole path can often times be treated physically as a single point. When the orbit is a perfect circle, the point representing that lamination is its radius, r. Our wheels would not be very strong, large or wide if they were very thin like a circle. But perfectly round wheels can be treated as a series of fat, wide laminations. Normally, we call them concentric cylinders - literally wheels within wheels.
Each fat, wide lamination or cylinder has an inner radius, r, an outer radius, R, and a width, w. To tell the cylinders apart, numbers are used to index them. The hub is the first cylinder, (r1,R1,w1). Outside that is the next the layer or cylinder, (r2,R2,w2). Usually, we want the outer radius of the inner cylinder to match the inner radius of the outer cylinder so R1 = r2. Continuing in this way, we work up to the wheel tread. Five cylinders were used to model an AWANA kit wheel and a Boy Scout kit wheel.
Note that the inner radius of the hub, cylinder 1, is the wheel bore. Note also that the hub width, w1, and the tread width, w5, are the widest.
When we model the physical properties of the wheel, mass, elasticity and moment of inertia, we will need to know the volume of each cylinder. This volume is the area of its face multiplied by its width, w. Its face area is the area of a disk with radius R minus the area of a disk with radius r. The area of a disk is the distance around it times its radius. The distance around it the same as that of a circle with radius R. That's pi times its raduis, R. pi is the ratio of a circle's circumference to its diameter which is 3.141592... The extra dots mean that the number continues.
Altogether, the expression for the volume, V, of the cylinder is then,
V = (RpiR - rpir)w, or simplified
V = wpi(R2-r2)
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |