| Grand Prix Racing - | The Science of Fast Pinewood Cars |
An essential object in the domain of Grand Prix racing is the car itself. Engineers love to draw their designs first. Then they calculate various performance factors. From these numbers, they determine what changes need to be made to increase the car's perfomance even more. It all happens on paper before any wood is cut!
But what measurements can be made that are useful for getting answers to car behavior on the track? What important aspects of your car's drawing will help you bring it into "reality"? A car is not as simple as the track we are using for our study. It has more parts and is influenced by physical forces so that it moves, spins, bobs and vibrates.
As your car races down the track, it is propelled forward by gravity. It is a rather gracious fact of the universe's design that for most purposes you can think of gravity as acting through a single point in your car. This very important point is called the center of mass of your car.
The center of mass is located in front of your rear axle and usually, but not necessarily, above it. When modeling the interactions between the track, your car and their physical energies and forces, the location of your car's center of mass must be known at all points along the track. The graph traced out by your car's center of mass is called its trajectory.
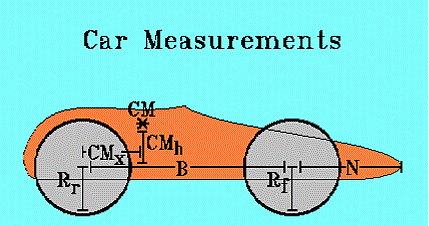
To find the car's trajectory, the car's geometry must be modeled. To start with, we need to know how far behind the starting line the center of mass, CM, is. The distance to it spans the nose of the car, N, and the base distance between axles, B, N + B; almost. The rear axle makes a convenient reference point since we know it is N + B inches behind the tip of the nose.
If you expect the front wheels to stay on the track, the center of mass can not be located behind the rear axle. But, we can measure the distance from the center of mass to the axle. We have to be clever about it so that we can use the distance not only to find how far from the front it is, but how high the center of mass is off the track too.
What we really get is two measurements. After you mark the center of mass, place your car on a flat surface. Hold a ruler horizontally over the surface with 0 next to a rear axle and 1, 2, etc. getting closer to the nose. Read the distance on the ruler by looking straight down over the point marked as the center of mass. This is CMx.
Now point the ruler straight up with 0 next to a rear axle. Look at the nose of your car toward its rear. Bend down so your eye is at the same height as the center of mass and read the vertical distance. This measurement is CMy. This way, CMx and CMy are almost always small positive numbers in inches.
If the front and rear wheels are the same size, the distance from the nose to the center of mass is N + B - CMx. If the sizes are different, we have to calculate an angle from the sizes to get the correct distance.
To know how far up the center of mass is, we need to know how high off the track the axle is. Well, that's just the wheel radius, R! If the front and rear wheels are the same size, the height is R + CMy. If not, we have to compute an angle to get the height.
If we give each radius a symbol, we can write an expression for the angle and for the distances. Let Rf be the radius of the front wheel and Rr the radius of the rear wheel. Using a little trigonometry, the angle turns out to be, * = arctan((Rf-Rr)/B). The distance of the center of mass to the nose is then (N+B-CMx)cos* and its height above the surface is Rr + CMysin*.
In order to study the sideways motion of the car, it will be necessary to know how far apart the wheels are. Since the front and rear wheels can have different spacing, we'll call these Sf and Sr, for spacing in front and rear. The spacing is measured from the inner edge of one hub to the other. The center of mass can also be off the center line of the car. We will measure this CMw (w for width) from the center line of the car.
For force considerations, the inner wheel or bore radius for the front, rf, and rear wheels, rr, need to be measured also. The following table shows the geometry that needs to be measured for the trajectory and track interactions modeled in this manual. Some are discussed in more detail in the model of Car Trajectory.

| SYMBOL | RANGE | UNITS | DESCRIPTION |
| N | 0 - 5.2 | inches | Length of car nose (front to front axle) |
| B | 1.2 - 5.8 | inches | Base length (front axle to rear axle) |
| CMx | 0 - 7.0 | inches | Center of mass distance in front of rear axle parallel to the car's base |
| CMh | -0.2 - 3.0 | inches | Center of mass distance above rear axle normal to the car's base |
| CMw | 0.0 | inches | Center of mass deviation from car's center line, right side (with front of car toward you) is positive |
| Rf | 0.59 | inches | Outer radius of front wheels |
| Rr | 0.59 | inches | Outer radius of rear wheels |
| rf | 0.049 | inches | Inner radius of front wheel bore |
| rr | 0.049 | inches | Inner radius of rear wheel bore |
| Sf | 1.6875 | inches | Separation or span between front wheels (inner hubs) |
| Sr | 1.6875 | inches | Separation or span between rear wheels (inner hubs) |
| * | -pi - pi | radians | Base slope |
Because your car interacts with the track and air around it, we need to talk about some physical properties of your car. These properties usually are not easy to measure directly. They describe how your car reacts in the presence of a force or other influence.
Much of this manual is concerned with friction. In order to describe friction carefully, we need to talk about friction and drag coefficients. A coefficient is just a number used as a multiplier. A drag coefficient tells how much force becomes friction.
Your car has six of these coefficients. "a" is for your car's drag form factor. "u" is for static friction. "nf" and "nr" are for axle friction. "uf" and "ur" are for tread friction. Again the small "f" and "r" are for "front" and "rear". The values of these coefficients can be compared or calculated with special equipment you can build or estimated by evaluating model equations after a race.
One dynamic parameter is also geometric. It is the area of the front shaddow of your car, A. Because it is a shape, it is possible to measure it directly by counting squares, mathematical formulas or by using a cutout and clay. "A" is used to determine the effect of aerodynamic drag on your car.
The center of mass of your car has been included in this car model. But it would do no good to kow its location without knowing the mass, m that it "centers".
| SYMBOL | RANGE | UNITS | DESCRIPTION |
|---|---|---|---|
| a | 0 - 1.5 | scalar | Aerodynamic drag coefficient |
| A | 0.92 - 7.5 | inches squared | Frontal crosssection including wheels |
| u | 0 - 1 | scalar | Coefficient of static friction |
| nf | 0 - 1 | scalar | Coefficient of front axle friction |
| nr | 0 - 1 | scalar | Coefficient of rear axle friction |
| uf | 0 - 1 | scalar | Coefficient of front rolling (tread) friction |
| ur | 0 - 1 | scalar | Coefficient of rear rolling (tread) friction |
| m | 0.01295 | ozs2/in | Mass of 5 oz car |
Only the wheels are left. Their geometry is a series of concentric rings of varying inner and outer radii and width. Moment of inertia and wheel weight are their dynamic parameters. The wheel model can be rather involved.
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |