| Grand Prix Racing - | The Science of Fast Pinewood Cars |
The first obstacle your Grand Prix car must overcome is just getting going! It must overcome inertia. The model developed here is too simple to get answers for a real Grand Prix car, but it shows the basic method used later in the much more complicated rolling models.
For a Grand Prix car, this force is a combination of at least two static forces. One opposes sliding between your wheel and axle. The other resists the intial rolling of your wheel's tread over the track. This could include a vertical force between the tire treads and track if they are "sticky" for some reason. Both oppose acceleration from rest.
But for now, just think about a block on a ramp and what happens when its about to slide.
Static Friction A force that opposes motion from rest due to contact between objects.

| F | Force |
| m | mass |
| g | Acceleration by gravity |
| N | Normal force, the force at right angles to the track |
| O | 'Theta', angle the ramp forms with horizon |
| H | Height of mass center at starting line |
| B | Length of ramp base |
| u | static friction coefficient |
Important expressions derived for this model include:
| Equations of Motion | F = m a = -mgsinO + umgcosO = 0 |
| static friction coefficient | u = H/B |
The force, F, of static friction, depends only on how hard the two objects are pressed together. For a car and track, this "pressing" force is supplied by the part of the car's weight that is supported by the track, the normal force. The degree to which the static friction depends on the normal force is expressed as a unitless quantity called the static friction coefficient. Static friction can then be written:
F = uN
F is the force produced by static friction in oz.
u is the static friction coeficient, no units (that is "scalar", it is a dimmensionless scaling factor).
N is the normal force holding the surfaces of the objects together in oz.
It is rather simple to derive an expression for the static friction of your car. Note however, this is not the same as your axle friction coeficient since the axle geometry will change the expression.
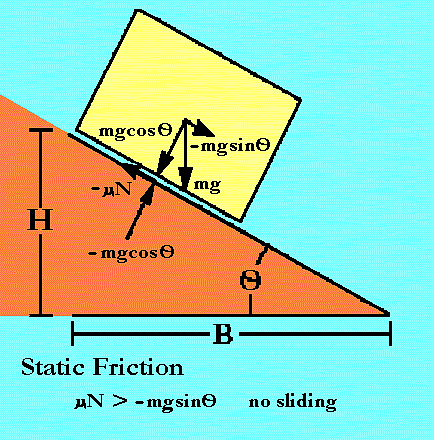
Imagine (or try this) a block at rest on a ramp inclined at an angle, O, to the top of a table. The forces on the block are the tangental part of the gravitational force and the opposing force of static friction.
If the tangental force was greater than the static friction, the block would be sliding. But it is at rest, so static friction must be greater than the tangental force.
As the ramp angle, O, is increased, the tangental gravitational force increases and the normal decreases. As the normal gravitational force decreases, so does the force of static friction that depends on it. This means a critical angle is soon reached where the forces are equal. Increasing the ramp angle any more initiates sliding.
To express these ideas we will need a few more symbols:
mg is the weight of your car in oz.
O is the angle of the ramp where the block begins to slide in degrees.
At the critical angle just before the block begins to slide, the equation of motion is
F = m a = -mgsinO + umgcosO = 0 (since there is no total force)
Rearranging
Static force = tangental force of block's weight
umgcosO = mgsinO
Solving for u, the static friction coeficient, and simplifying,
u = tanO
For a ramp, tanO = H/B,
the height of the ramp end, H, divided by its base length, B, so
u = H/B
In practice, this means the block that initiates sliding at the lower angle, O, has the lesser amount of static friction to overcome.
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |