| Grand Prix Racing - | The Science of Fast Pinewood Cars |
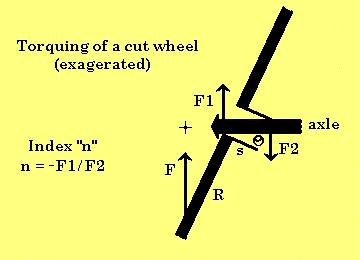
When tread is cut off a wheel, often the wheel becomes torqued on the axle. This happens because the tread helps keep the center of upward force centered on the axle between the ends of the wheel bore. Without the tread on one end or the other of the wheel, the force that the track exerts on the thin tread is concentrated on the edge of the bore on the side of the wheel that still has tread.
If your wheel's bore sticks out on the tread side, the problem of torquing may not occur unless your axle has enough "play" to let the wheel bore tip on it.
But kit wheels often have recessed bores on the side where the tread is left after cutting. So most often, they will torque on the axle if tread is removed to a point near the recess line.
Most of the time, there is enough "play" in the wheels for the wheel to look slanted in or out when the car is placed on a flat surface. If you can't see any slant, you need to look closely at the opposite ends of the wheel bore - if it's possible. If you see the axle touching the top of the bore on one end and the bottom of the bore on the other, your wheel is torquing!
This model derives the torquing forces at either end of the bore. You will see why torquing is bad and how much it can affect your car if you can measure the slant angle. You may also gain an appreciation for a technique that helps simplify some calculations, indexing or quantizing.

| F | Force on edge of wheel on track |
| F1 | Force on bore at wheel face |
| F2 | Force on bore at wheel hub |
| R | Outer wheel radius minus inner wheel radius |
| s | Bore shaft length |
| O | 'Theta', angle the axle forms with the wheel bore |
| n > 1 | An index indicating F1 is n times stronger than F2 |
Important expressions derived for this model include:
| Stasis | F1RsinO + F2(RsinO+s) = 0 and F = F1 + F2 |
| Force Ratio | F1 = -nF2 |
| F1 | F1 = Fn/(n-1) |
| F2 | F2 = F/(n-1) |
| O | O = arcsin(s/R(n-1)) |
This model begins as do many others by writing the equations of motion as simply as possible. In this case, a torque develops about the contact point on the track. When the wheel bore is not in full contact with the axle it touches it at two points and there is no net rotation. The wheel bore touches the axle only at its extreme ends and transmits forces through them.
To create a model based on static torque, we find a point about which to compute the torques that makes the expressions as simple as possible. A point on line with the axle but out from the hub was chosen. When the wheel is not changing its angle to the axle (no net rotation) we can write:
F1RsinO + F2(RsinO+s) = 0 where s is a good approximation of its portion of the lever arm distance to keep the expression simple.
Which is a relationship between the two forces F1 and F2
F1RsinO = - F2(RsinO+s)
To show how they are related more explicitly, we take the ratio of F1 to F2
F1/F2 = -(RsinO+s)/RsinO
Simplify
F1/F2 = -1 - s/RsinO
Now define an index, n, to make it easier to interpret this relationship since we won't be measuring F1 and F2 directly.
Let n = s/RsinO + 1 for integers n greater than 1, (at n = 1, sinO would need to be infinite which can't happen)
Then we can substitute this index, n, for -F1/F2 and get a mental picture of how various model parameters change with it. For example, solve for theta, O, the torquing angle of the wheel in the expression for n.
O = arcsin(s/R(n-1))
Now, let's see what F2 looks like in terms of this n. The total force on the edge of the wheel where it touches the track must be
F = F1 + F2
Substituting F1 = -nF2
F = -nF2 + F2
Simplify and swap sides
F2(1-n) = F
Divide through to isolate F2 (to a point)
F2 = -F/(n-1)
What is F1 in terms of n? This time substitute F2 = -F1/n
F = F1 - F1/n
Simplify and swap sides
F1(1-1/n) = F
Normalize the term in parentheses so the n can be divided out
F1(n-1)/n = F
Now multiply and divide through to isolate F1
F1 = Fn/(n-1)
Axle friction is the total amount of friction experienced by your wheel as the result of the wheel rubbing against its axle. The forces F1 and F2 both contribute directly to the axle force that becomes friction. Though F1 + F2 = F, and F1 is in the opposite direction of F2, when the axle friction is calculated, it is the absolute values of F1 and F2 that are used to calculate that friction. This is because there are equal and opposite forces pushing against them, these stresses create the force at right angles to the axle that create the friction.
As noted above, F/F1 = (1-1/n) is less than one by 1/n, so F1 is already, by itself, greater than F! When the magnitudes (absolute values) of F1 and F2 are added to get the total axle friction, they give a result greater than F.
|F1| + |F2|= Fn/(n-1) + F/(n-1) (the bars, |X|, indicate absolute value)
Simplify to get
|F1| + |F2|= F(n+1)/(n-1)
This expression shows an increase in F of (n+1)/(n-1) for n > 1. At n = 2, the lowest ratio in our index, the friction causing force is three times greater than that of a wheel that is flat on the track. That would be a wheel slanted at an angle of about 27.5 degrees, definitely noticeable. As n increases, O decreases. At n = 27 (about 1 degree of tilt) the friction force is about 1.08 times that of the "squared up" wheel. The extra friction force is less but probably still more than that gained by decreasing the wheel's moment of inertia by cutting the wheels.
|
Where is the critical slant angle that makes it worth while to cut tread? One can use the closed model to simulate the effect of wheel torquing on race time. The factor for the increase in F of (2RsinO/s + 1) or (n+1)/(n-1) can be directly multiplied by the axle friction coefficient to get a new one that accounts for this problem. With these facts, we can stage a virtual race to find the critical angle, O.
First, run the race with a reference car and the perfect cut wheel car. Next, change the amount of axle friction on the "perfect" cut tread car so it's time is as close as possible to the reference car. This is where a computer program really helps! Then determine the increase factor in the axle friction needed to match the race times, call it z, and solve z = (n+1)/(n-1) for n.
z = (n+1)/(n-1)
Multiply through by n-1 and distribute
zn - z = n + 1
Subtratct n from both sides and collect terms in n
n(z-1) - z = 1
Add z to both sides
n(z-1) = z+1
Devide through by z-1 and amazingly, the result looks like we just swapped n for z.
n = (z+1)/(z-1)
Now, solve for O using the equation for O(n) from above and call it Oc (c for "critical"):
Oc = arcsin(s/R(n-1))
That is how you can find the critical angle. A slant less than Oc is worth it, otherwise, it is not.
| [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |