| Grand Prix Racing - | The Science of Fast Pinewood Cars |
Though your Grand Prix car may not free fall from the starting line, it most certainly does fall! It's fall is "cushoned" or constrained by the ramp so the end result is not quite so disasterous depending on how steep it is. Though the energy is converted in much the same way as in free fall, timing is delayed and the distance of travel is greatly increased. Such effects are a true warping of space and time from the perspective of the energy involved!
Galileo Galilei used ramps to further investigate the results so dramatically demonstrated at the Tower of Pisa. As an application of this model, it can be shown that the ramp "magically" increases the distance and time of the "fall" though the speed of the fall remains the same at any vertical position! It is as if the ramp has distorted space and time for the falling object. The concepts of arc parameters, moment of inertia and pathagorus's theorem are used. A mathematical expression for a form of the conservation of energy is used to derive the physical parameters; energy, speed, time and distance. The equations of motion are examined for insight on force decomposition.

| E | Total conserved energy |
| U | Potential energy |
| T | Kinetic energy |
| F | Force |
| m | Mass |
| g | Acceleration by gravity |
| v | Velocity (strickly speaking, speed) |
| L | Length of ramp |
| y | Distance along trajectory |
| O | 'Theta', angle the ramp forms with horizon |
| t | Time from start of fall |
| Ft | Force along the ramp surface |
| Fn | Force at right angles to the ramp surface |
Important expressions derived for this model include:
| Energy Relation | E = -mgLsinO = -mg(L-y)sinO + mv2/2 |
| Equations of Motion | Ft = m a = -mgsinO, Fn = 0 |
| Time of fall | t(y) = \[-2y/gsinO] |
| Speed of fall | v(t) = -gsinOt |
To begin this model, we start by writing some parameters and relations for a simple ramp.
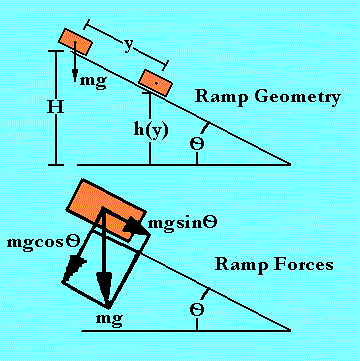
A ramp has a starting height, H, a surface length, L, and a downward slope, O (theta). Note, the ratio of ramp height, H, to its length, L, is,
H/L = -sinO or O = -arcsin(H/L) only O < 0 is down hill, O > 0 is an up hill ramp. We only want to consider down hill motion in this model, so sinO is always negative. This leads to positive expressions with "minus" signs in them like:
H = -LsinO which is greater than zero.
The car is modeled with no friction on this simple ramp. On the ramp, the height the car has left to fall is "h" and the distance traveled along the ramp surface is "y". The distance travelled along the surface, y, can be expressed in terms of the other ramp and car parameters (symbols) as:
y = -(H-h)sinO or y = L + hsinO
To model the height left to fall in terms of distance traveled, we write
h(y) = -(L-y)sinO
Again the potential energy of the car is modeled as mgh. But this time, h is in terms of y, h(y). Also, the initial potential energy, mgH, is -mgLsinO, since H = -LsinO. Kinetic energy is present in the same form as in the free fall, but the velocity is not in the direction of h, but y, along the ramp. The energy relation is:
_______Potential_______ + Kinetic Energy
Track Car Car
E = -mgLsinO = -mg(L-y)sinO + mv2/2
In order to solve for the velocity, v, group terms in sinO and the velocity squared, v2,
-mgysinO = mv2/2
Solve for velocity, v, in terms of position from the top of the ramp, y,
v(y) = \[-2gysinO]
Separate variables in position, y, and time, t, and integrate,
/ y / t
| dy/\[y] = \[-2gsinO] | dt
/ 0 / 0
/ y
| dy/\[y] = 2\[y]
/ 0
/ t
\[-2gsinO] | dt = \[-2gsinO]t
/ 0
Putting these results together:
2\[y] = \[-2gsinO]t
Solve for time, t, in terms of position, y,
t(y) = \[-2y/gsinO]
Solve for position, y, in terms of time, t,
y(t) = -gsinOt2/2
Solve for speed, v, in terms of time, t, by taking the derivative of position in terms of time, y(t), with respect to time, t,
v(t) = -gsinOt
Solve for acceleration in terms of time, t, by taking the derivative of speed in terms of time, v(t), w.r.t. t,
a(t) = -gsinO
Knowing the acceleration along the ramp, we could write the equation of motion along the ramp (tangent to it) as:
Ft = m a = mgsinO
But now there is another equation of motion which is at right angles to the first. It expresses the normal force of the ramp against the car. But all of these forces must cancel perfectly because the ramp does not flex or move under the influence of the car passing over it. This is an example of Newton's Third Law.
Fn = m a = mgcosO - mgcosO = 0 (normal)
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |