| Grand Prix Racing - | The Science of Fast Pinewood Cars |
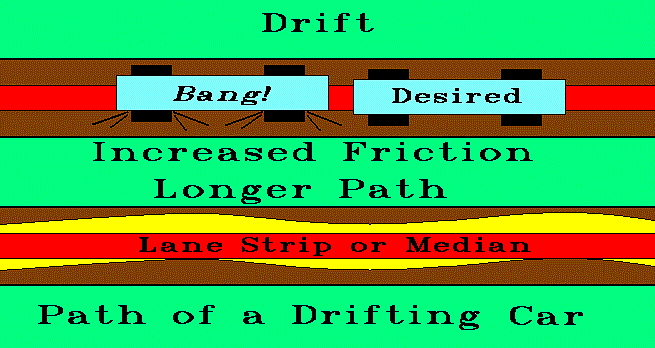
The purpose of the lane median is to guide your car down the track if it "loses" its way. Unfortunately, the price of that guidance is a little energy. For cars that only brush the median and continue, this is not much of a penalty. But for those that persist in errancy, they can fall way behind in the pursuit of their trophy.
Most collisions on the Grand Prix track occur with the lane median. Behavior during the collision lies on a spectrum from elastic behavior to inelastic. The alignment of your wheels and how much they can play on the axles probably determines which will be the dominant behavior. Poor alignment and lots of play are likely to lead to more inelastic behavior than closely-held, straight wheels.
Here you will see what must happen for a collision to take place and how bad it can be. Forces (that is dynamics) are the main focus of this page. Not all factors that might be important in a Grand Prix median collision are easily modeled. For those only descriptions are rendered.
Here are a few dynamics that are more easily modeled.
| r | Coefficient of median friction |
| P | Push force at right angles to the median |
| O | Drift angle less than 0.34 radians (20 degrees) |
| L | Distance of travel |
| F | Forward force of the car |
| u | Coefficient of tread friction |
| S | Axle separation |
| D | Axle drag |
| R | Outter wheel radius |
| r | Inner wheel radius |
| m | Mass of car |
| g | Gravitational acceleration |
| T | Torque |
| I | Moment of inertia |
| @ | Angular acceleration |
| a | Linear acceleration |
Important expressions derived for this model include:
| Median Friction | rFO |
| Work on median by the car | rFLO2 |
| Tread friction increase from toeing | 1 + O |
Wheel alignment drift can be measured and corrected if you are diligent. By "wheel alignment" I mean how straight your wheels line up along the track. Its toll on your car depends on many things, but the more deviation from perfectly straight, the more the car will pull to one side.
How much does it pull to one side? When your car rides against one side of the lane median, the friction caused can be modeled as sliding friction. The friction force would be the rubbing coefficient times the force the car exerts on the median at right angles to it; just the sideways push. We could write:
Median Friction = rP for r = the rubbing coefficient, P = the sideways push
What is the sideways push? When wheels are misaligned, they direct the momentum of the car to the side at some usually small angle, O, over some distance of travel, L. So the sideways push-force P is sinO times the forward force, F, of the car.
P = FsinO for F the forward force of the car.
Making this substitution,
Median Friction = rFsinO = rFO for O < 0.34 radians
When the car is up against the median, the wheels must slip a bit in the direction of the median because they can not go through it. Work is done through the distance of the slip by the median force on the inner edges of the wheels. So we can write the work done as
Work on median by the car = rFLsin2O = rFLO2 for O < 0.34 radians
For a car with a forward force of F=1.5 ounces (fairly typical), a rubbing coefficient of r=0.5 and a sideways deviation angle of O=0.34 we get
Median Friction = 0.5*1.5*0.34 = 0.255 ounces
Over a distance of one foot, L = 12,
Work on median by the car = 0.5*1.5*12*0.34*0.34 = 1.04 ozin
The total energy available to a car on the official AWANA track is about 200 ozin.
|
Over a track length of 30 feet, that would be about 15% of the car's energy lost by rubbing the lane median.
Misalignment may also cause an energy loss that strictly speaking is not drift but a type of friction. It occurs when both of the front or back wheels are angled in or out from the body center line. One wheel pulls left, the other right. Neither wheel wins the tug-o-war, but a sliding friction force is exerted across the track as the wheels spin at an angle to it. The resulting force may not actually cause a drift to the left or right, but the wheels will act like they have more tread friction than other cars.
Assuming the left and right wheel have the same but opposite deviation angle, O, from straight, over a distance, L, the wheels will each slip a distance of LsinO without actually causing movement to either side. The friction force along the track is uF, where u is the coefficient of tread friction and F is the force of the axle and wheel weight on the tread.
The effective work done is uF(L+LsinO) instead of uFL.
So the tread friction increases by a factor of
uF(L+LsinO)/uFL = 1+sinO
For small angles (less than about 0.34 radians or 20 degrees) in radian measure, this can be closely estimated as
1+O
You would notice deviations of 20 degrees and tread friction that was 1.34 times greater.
|
When your car hits the lane median at some speed and angle, it's usually the inner edge of the wheel tread that hits first. That causes a breaking action on the tread by rubbing it and stops the wheel from moving sideways. The body of the car continues to move sideways toward the median until the axle hub hits the wheel bore and causes more rubbing - another breaking action. This friction is multiplied if the wheel's tread edge touches near the front and near the rear and if the other wheel on the same side also bangs into the median. The result is a lot of rubbing that increases with the sideways force of impact. That impact is dependant on the collision angle and the car's speed.
The details of the collision are scary enough, but what happens next depends on a number of things that you did to your car while putting the wheels on. More study needs to be done on the exact relationship of what you did to how it behaves, but it's pretty easy to see the final behavior. See the models for more elastic and more inelastic behavior.
If your wheels are not all touching the track, two may touch intermittently on a diagonal and cause the car to rock like a see-saw. At the moment when one wheel touches it shares the tread and axle friction with the other wheel on the same side. The torque of paired wheels tend to cancel. But the odd wheel creates a small torque that tries to turn your car to the same side it is on. See the table below for the direction of the turn depending on the location of the odd wheel. "Left" and "right" are designated looking at the front of your car as it races toward you.
| Odd Wheel Touching | Turn to Left Side | Turn to Right Side |
|---|---|---|
| Front | Left | Right |
| Rear | Left | Right |
Once lifted, all the friction on that side rides on the other wheel. That wheel now produces a side ways torque on the car opposing the torque of the other touching wheel. So the amount of friction and side ways torque endured by the wheels is constantly changing. This can cause your car to wobble from side to side costing extra energy due to the lengthened path it must travel - not to mention median collisions.
As one wheel touches down, three are on the track. Each wheel produces tread and axle drag. But there is a more serious problem than that. Each time a bobbing wheel touches the track, it spins up and the diagonally opposite wheel spins down. How much spinning up and down takes place depends on how long and how hard the force of contact is. Each time a wheel spins up to track speed from a stand still, it takes Iw2/2 ozin of rotational kinetic energy from the car; I is the moment of inertia of the wheel, w it's rotation rate. The wheel spinning down takes no energy, but loses what energy it has; it will take energy to spin it up again.
If the car rocks back and forth between the two wheels, energy will be continually lost as the wheels are spun up again and again. How long does it take a wheel to spin down to a stop? The answer for a wheel spinning at maximum speed is a few seconds. So the bobbing wheel will not stop spinning before it is spun up again. That means some energy is saved.
As bobbing rocks the car, the car is losing energy in rocking also. This time, I, is the moment of inertia of the car around a diagonal axis. Loss in body kinetic energy is about Iw2/2 for w the average magnitude of the angular speed of rocking.
At the beginning of the flat part of the track, how much energy is lost to bobbing at its natural pendular frequency and what is the turning torque, T, each time a wheel touches?
Let D be the axle drag of the unpaired wheel of outer radius R and bore radius r and let S be the across track separation to its opposite, lifted wheel. Assuming the center of mass of the car is in the middle, half of the car's weight, mg/2, is on this wheel. The sideways torque, T, pushing this wheel to the side is then
T = DS/2 = (nmgr/2R)*1.8/2 = n5*0.049/2/0.591*0.9 = n*0.19
For a friction coefficient of n = 0.2, the torque is 0.038 ozin. But the torque can be expressed as the car's moment of inertia, I, times its angular acceleration, @. A typical value for a car's sideways moment of inertia is about I = 0.014 ozins2.
T = I@, so, @ = T/I = 0.038/0.014 = 2.71 rad/s2.
The linear acceleration at a point on the tread is a = @R.
@R = a = 2.71*0.591 = 1.6 in/s2.
So the axle is constantly decelerated by 1.6 in/s2 more than the two paired wheels that touch the track. This amount of turning affects the car only while the wheel touches. If it touched for a tenth of a second, 1.6*0.1 = 0.16 in/s loss of speed on the same side as the wheel. That's 0.16*0.1 = 0.016 inches behind. Hardly noticeable. But this is just the sideways torque due to axle friction. Torque from uneven tread friction can be treated similarly to give numbers of similar size. Torque from spinning up the wheel would also add to this a little.
To estimate the torque of axle friction slowing a wheel on the flat (spinning down) write the torque from the drag acting through the wheel bore radius, r.
T = Dr = I@ = Ia/R so Dr = n5*0.049/2 = 0.000048a/0.591 so a = n 5*0.049*0.591/(2*0.000048) = n1508.28
a = 0.2*1508.28 in/s2 = 301.7 in/s2
That's 301.7*0.1 = 30.2 in/s or 30.2*0.1 = 3 inches in a tenth of a second.
Jumping The Track
The wheel may also jump up if there is a jagged edge or rough spot on the median wall. If the edge of the wheel catches it, it will want to rotate about the protrusion and lift the car axle up. This situation is the same used to derive the expression for rolling (tread) friction. But in that case we took a limit letting the bump size decreased to zero. This time, the bump size is much larger.
From the rolling friction derivation we had the expression at the point where the horizontal force, F, was just about strong enough to lift the wheel over the bump:
0 = Ws-Fq which is just Fq = Ws
From the geometry of the wheel and bump, we can write s the distance from the center of the wheel to the bump in terms of the distance from the wheel center to the top of the bump, q. q is the wheel radius, R, minus the bump height, h, (that is, q = R-h).
s = \[R2-q2]
Substituting in the force equation for s we get,
Fq = W\[R2-q2]
Devide through by q to obtain,
F = W\[R2/q2-1]
This is the minimum amount of horizontal force required to begin lifting the wheel over the bump.
The actual vertical force developed must be determined from the change in momentum of the car in the vertical direction and the amount of time required to lift it. Complexity creeps in because only one side of the front or rear of the car is lifted initially.
To get at the change in momentum, we determine the vertical component of the speed. If the car was traveling at speed, v, when the bump was encountered, the distance h would be covered in about s/v seconds, assuming the car did not slow down much. This makes the vertical part of the speed for the wheel about,
vh = h/(s/v) = hv/s = (R-q)v/\[R2-q2]
Recognize the difference of two squares (that is, (X2-Y2) = (X-Y)(X+Y)) to get,
vh = (R-q)v/\[(R-q)(R+q)] = v\[(R-q)2/(R-q)(R+q)] = v\[(R-q)/(R+q)]
With the wheel on top of the bump, it is likely supporting a significant part of the car's weight. For an average car, assume for the moment that the weight borne is mg/2 since only the wheel opposite the one touching the bump is in the air. The work done - which is the same as the energy lost - is just that required to lift the front or rear of the car about h inches up.
work = mgh/2
If the force is greater than the minimum required to lift over the bump, then more work is done as the car jumps in the air. On the way down, the energy loss is powered by gravity, so it isn't really lost to the car.
The initial momentum of the affected side of the car over the bump likewise depends on the geometry and weight distribution of the car. If the supported mass is m/2, then the change in vertical momentum in time s/v is about mvh/2. An estimate of the average force of the jump is then the change in momentum divided by the duration of the lift,
mvh/2/(s/v) = mvhv/2s
An estimate of the acceleration is the force divided by the mass,
a = 2(mvhv/2s)/m = vhv/s = v2\[(R-q)/(R+q)]/\[R2-q2]
Simplify using the difference of squares
a = v2(R-q)/(R2-q2) = v2/(R+q)
So the average force is about
F = mv2/2(R+q)
For a mass of m = 0.01295 ozs2/in, speed of v = 160 in/s, AWANA kit wheel of radius R = 0.59 inches and vertical bump offset of q = 0.465 inches (that's an eighth inch bump), we get an average force of,
F = 0.01295*(160)2/2(0.59+0.465) = 157.1 oz
That's about ten pounds of force pushing on the bump! In terms of acceleration, it's 31 g's! If the car's center of mass is near the rear axle (or the car is light) and one front wheel jumps, the acceleration is greater than for a more centered car. That car might roll off the lane and into other cars or drop to the floor. Perhaps you've seen it happen?
| [Next Section] | [Pit Area] | [Title Page] |
| Grand Prix Racing - | The Science of Fast Pinewood Cars |
| Copyright © 1997, 2004 by Michael Lastufka, All rights reserved worldwide. | |