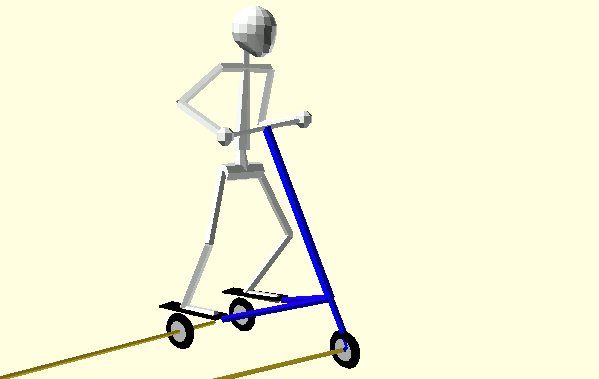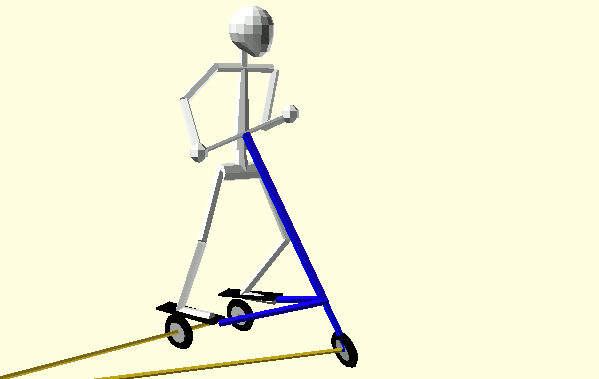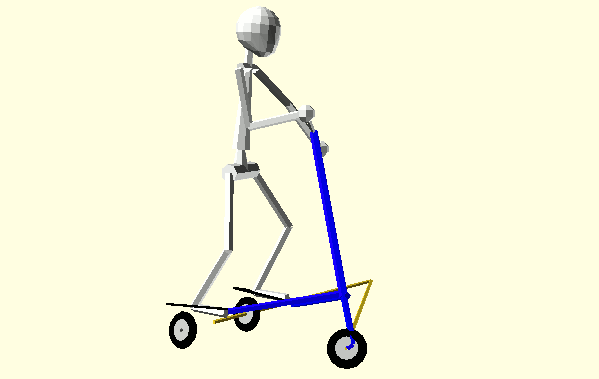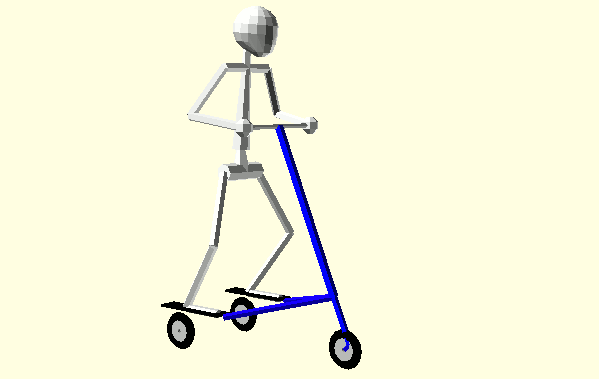
Animation 1: Hip and Shoulder Rotation with Synchronous Turns and Turn Radii
There are many ways people ride a Trikke and even more ways they think they ride. Spin of the Rider's body is the engine that drives the ride. The Parallel Axis Theorem and the Law of Conservation of Angular Momentum conspire to define the limits of these techniques. Drive-cycles split neatly into two phases in each half-cylce as the serpentine turns of the Trikke pass striaght. Four derived conservation equations apply to the two phases of two primary riding styles and two variations. Analysis reveals that the Rider is free to generate as much angular momentum as possible, enhanced by delayed steering in Phase I. Exactly half of his angular momentum is reflected to the rest of the system. Any increase in Phase II is wasted, but the other half of the Rider's angular momentum transfers to the Trikke and Rider around the turn center in Phase II. These results inform Trikke Riders desiring to improve their riding goals with a solid physical understanding previous unknown in the literature.
Riding a Trikke is about angular momentum management through body rotation. When a Rider rotates around his natural vertical rotation axis, he is spinning. Spinning with appropriate arm and leg tension with some pushing and pulling drives a Trikke. The Trikke does not spin around it own axis, it rotates around a turn center located to one side or the other over a meter away. Since the Rider is holding onto the Trikke, she is also rotating around the same turn center at the same angular velocity. In this role, she is a Glider.
Applying the Parallel Axis Theorem and the Law of Conservation of Angular Momentum to the Rider's spin results in the Trikke and Rider rotating around the turn center as if attached to a virtual armature. The Rider must engage the Trikke handlebar grips and foot decks with adequate tension to couple body spin with the Trikke. Movements can be performed to decouple the relationship (like becoming a "rag doll", waving to someone or jumping on the decks), but unless stated, assume enough tension is present.
Two rotating and one spinning object must account for the angular momentum of the system because angular momentum is physically conserved. The two rotating objects have a common angular velocity but the thrid object can spin independently. The Rider is the third object and one of the two rotating objects, the other being the Trikke. Two roles played by the Rider include one to drive the Trikke and one to glide with the Trikke. When refering to the Rider in this glider role, she will be called the Glider. A fourth quantity of angular momentum is a constant; the total amount in the system. Each harbors an amount of angular momentum using the following symbols:
To be conserved, they must balance like this:
Equation 1: Total Angular Momentum is conserved
These angular momentum terms Lx may be positive or negative depending on their direction of rotation. Positive for counterclockwise rotation; negative for clockwise. Generally, if one term is non-zero, one or both of the others must also be non-zero and rotating in the opposite direction to balance the relationship. They decompose further using the Parallel Axis Theorem and basic definitions.
Equation 2: Angular Momentum actors in terms of Moment of Inertia and Angular Velocity
All of these symbols represent positive quantities except for the angular velocities, ωr and ωt, which can be either positive or negative. Note the single expression in ωr; the Rider's spin velocity. There are two terms in ωt; the Trikke and Glider's rotation velocity. Ir represents the Rider's and Glider's moment of inertia and Mr their mass since they are different roles of the same person. It and Mt are the Trikke's moment of inertia and mass, which are much less than the Rider's. R is the distance from the Trikke-Glider center of mass to the the turn center.
Rewriting Equation 1 in terms of the velocities, the result is:
Equation 3: Conservation in terms of moments of inertia and angular velocities
It is much easier for a Rider's body spin to rotate a Trikke around the turn center through tensioned arms and legs than for the Trikke and Glider to rotate the Rider around his body axis. First of all, the Rider usually has five or more times the mass and higher inertial moment. Then the Rider would have to move in such a way as to absorb Trikke-Glider rotation around the turn center. It is not clear that it is even possible without the Trikke comming to fast stop to cause the angular momentum to transfer - like getting hit by a handlbar. This means that angular momentum can only flow from the Rider to the Trikke-Glider, not the other way.
Equation 4: Trikke-Glider Moment of Inertia
With Equation 4 in hand, all of the Trikke-Glider positive constants are combined into a single quantity, Itg to make interpretation of the following equations more obvious. For the sake of argument, R, the distance to the turn center, may be considered constant as it will not affect the conservation relations. For Rider spin opposite to Trikke-Glider rotation, the equations are:
Angular momentum built up by the Trikke-Glider can be considered external at appropriate points in the analysis. It becomes part of the dynamics of the global reference frame and is ignored in the local analysis frame. Global variables, when needed are capital symbols with corresponing local variabls in lower case, except for the variables L, which are local. The local frame rotates with the Trikke-Glider at an angular speed of Ωt due to built up angular momentum.
The two angular velocities Ωt and ωr can either be aligned in the same direction or in opposite directions. When aligned, Equations 5a and 5b result, otherwise Equations 6a and 6b for opposing directions. The a and b correspond to
Note, initially in a half-cycle phase, local ωt = 0 but its global counterpart, Ωt, may not be.
Equation 5a: Reflection - Opposite Angular Velocities with no initial Angular Momentum
Equation 5b: Transfer - Opposite Angular Velocities with initial Angular Momentum
For Rider spin in the same direction as Trikke-Glider rotation, the equations are:
Equation 6a: Reflection - Aligned Angular Velocities with no initial Angular Momentum
Equation 6b: Transfer - Aligned Angular Velocities with no initial Angular Momentum
Steering and body spin begin in the same direction at the start of each half-cycle. Each half-cycle has two Phases separated by the Trikke turning through straight. Amazingly, the following concludes that exactly half of the Rider's angular momentum is reflected to the Trikke-Glider in Phase I and the other half transferred in Phase II. If the Rider attempts to increase his spin in Phase II, his efforts are wasted. Some form of this gait is typical among Trikke riders. Animation 1 illustrates the technique and shows the alternating and dynamic location of the turn center through the intersection of axle rays.

Animation 1: Hip and Shoulder Rotation with Synchronous Turns and Turn Radii
Consider the state when the Rider stops spinning to the left and the Trikke is turned to the left. The Trikke-Glider has all of the angular momentum the Rider none. If the Rider does nothing, the Trikke-Glider coasts to a stop, but does not affect the Rider's zero-spin becuase standing on the decks is not the right kind of coupling to cause the Rider to spin around his body axis. When considering momentum change, the amount owned by the Trikke-Glider is assigned to the global rotation of the rotating local analysis frame.
With no angular momentum in this local rotating frame, the Rider now begins to spin and turn the Trikke to the right. The Trikke does not turn to the right immediately, it must "roll out" of the left turn; pass straight ahead; and then begin its actual turn to the right. During the roll out, the Trikke is decreasingly turning left, the opposite direction from the Rider's body spin.
In this first Drive Phase, from when the Rider begins spinning and turning to when the Trikke is turned straight, the local angular velocities are opposite. When the system has no angular momentum in the local frame, Equation 5a above indicates that opposite velocity orientations cause the momentum terms to grow or to dissipate together, equally. What happens to one is reflected in the other. Since Rider spin increases, the Trikke-Glider also increases rotation in the opposite direction. The Rider supplies equal angular momentum to himself and the Trikke-Glider. Half of his energy goes into accelerating the Trikke-Glider and half his own spin.
Turning straight, the Trikke and rider enter the second drive phase. Now the Rider has half of the angular momentum and the Trikke-Glider has the half the Rider gave it. Since the Trikke momentarily travels straight, it no longer has a turn center to rotate around; hence no angular momentum in the global frame. It has all become linear momentum. At this point, the local frame angular momentum from the Rider can be added into the global frame as linear momentum. Invoke a new local frame to continue analysis, one in which the Rider has all the angular momentum, turning to the right. As the Trikke continues to turn past straight, it begins to rotate in the same direction as the Rider's spin. Globally, the linear momentum becomes angular again, but still has no bearing on the local analysis frame rotating with it.
Locally, the Trikke-Glider starts with no rotation but the Rider continues to spin from Phase I. Since spin and rotation are aligned, Equation 6b applies. As Rider spin decreases, Trikke-Glider rotation must increase. This continues until there is no more Rider spin. He has stopped spinnning and all of his angular momentum has transferred to the Trikke-Glider. In summary, the Rider's angular momentum transferes to the Trikke as he stops spinning.
If the Rider increases spin over that which he started with in Phase II, Equation 6b implies that Trikke-Glider angular momentum must increase in the opposite direction in the local frame. This sounds counter productive, but is soon corrected as the rider must stop spinning at some point. During the slow down, the Trikke-Glider angular momentum in the local frame becomes the initial amount in the same direction. Phase II can produce no more angular momentum than it started with. Ultimately, All of the Rider's angular momentum is added to the Trikke, exactly half in Phase I and half in Phase II.
Steering and body spin begin in opposite directions at the start of each half-cycle. Each half-cycle has two Phases separated by the Trikke turning through straight. Oddly, the following concludes that exactly half of the Rider's angular momentum is removed from the Trikke-Glider in Phase I and the other half transferred in Phase II for a net zero gain. If the Rider attempts to increase his spin in Phase II, his efforts are wasted. Though there is no net gain of system energy with this gait, it may be a welcome exercise variation to break up the cadence. Animation 2 illustrates the Rider's actions in this technique.
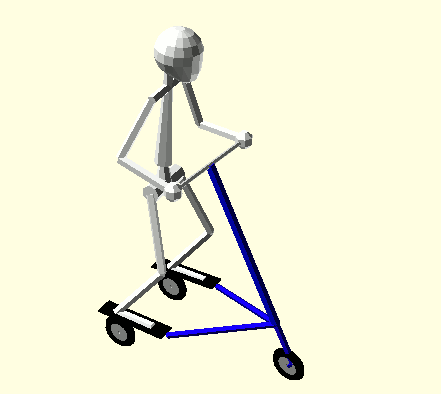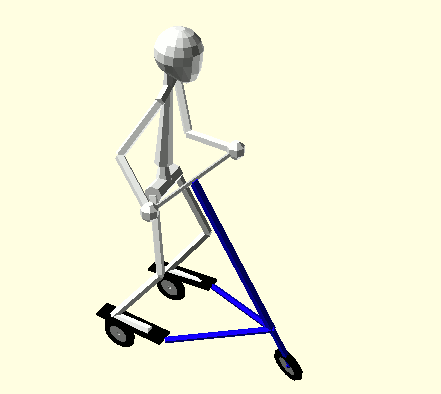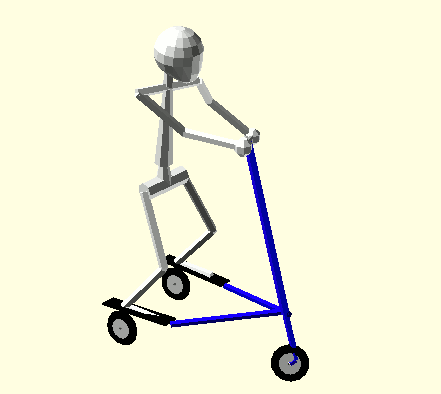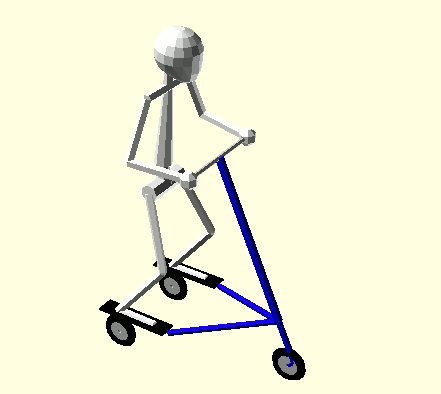
Animation 2: Hip and Shoulder Rotation with Opposite Turns
What happens when steering and spinning are exactly opposite? The Trikke-Rider System already has a quantity of angular momentum steering to the Left. As before, relegate it to a global Frame and let the local analysis frame rotate with it so that in the local frame the Trikke-Glider has no angular momentum. The Rider stopped spinning to the right and is about to spin back to the left. With these initial conditions Equation 6a applies.
Equation 6a indicates that once the Rider starts spinning to the left, the Trikke-Glidder must start rotating to the right, even though the Trikke is decreasingly rotating to the left. Note that the Trikke-Glidder rollout from the left to the right happens in the global frame. So, a Trikke-Glidder rotation to the right in the local frame can happen. It does not mean that some of the Trikke-Glider's momentum was borrowed from the global frame, it was increased in the opposite direction in the local one, which knows nothing of the global frame momenta. It does mean that as the Rider increases spin, the Trikke-Glidder increases counterrotation to the global frame, helping the Rider turn the handlebars to complete the rollout quicker.
Similar to the Synchronous Steering Riding Technique, when the rollout is complete, the Trikke-Glider travels forward for a moment, the turn center flips sides and the Trikke-Glider starts to rotate around it. The global angular momentum converted to linear momentum and back with opposite sign. The Trikke-Glider angular momentum from the first phase must be subtracted because of direction from the golbal quantity and a new local frame established.
With this Contra Steering technique, the local frame, traveling on the reduced global rotation, the Rider now has all of the local angular momentum and the Trikke-Glider has none. They rotate in opposite directions invoking the transfer relation of Equation 5b. Again as in Phase II of the Synchronous Steering Riding Technique, reduction in Rider spin means increase for the Trikke-Glider rotation in the opposite direction. When the Rider stops spinning, all his angular momentum has been transferred.
If using this technique, the Rider generates all his angular momentum by the time he steers straight, then exactly half of his momentum from Phase I is subtracted from the Trikke-Glider's global momentum and the other half is added in Phase II. That means no net angular momentum is gained. The Rider might as well have coasted.
Note, that trying to increase angular momentum in Phase II means, via the minus sign in Equation 5b, that the Trikke-Glider's angular momentum must increase in the same direction, not the opposite. However, as before, the Rider must stop spinning and eventually all the initial angular momentum transfers. Again, no more and no less can be transferred than is initally available.
Otherwise similar to the Synchronous Steering Technique, body spin begins before steering in the same direction; illustrated in Animation 3. Phase I initial conditions are the same, so the result is a longer time to conjure a spin, ideally a stronger spin. Since the Trikke-Glider still rotates around a turn center, Equation 5a still applies. Phase II is identical. But if the Rider completes body spin before passing straight (the onset of Phase II), there is no net angular momentum in Phase I to transfer in Phase II.
Delaying steering in the Contra technique merely builds more of a decrease in angular momentum to be undone in the Phase II transfer. But if spin completes before Phase II, again there is nothing to transfer.
Modifying the Synchronous Steering Technique with delayed steering may help pump extra energy into the ride when the delay is not too long. It doesn't help the Contra technique.
Animation 3: Hip and Shoulder Rotation with delayed Turns
Another technique similar to Synchronous Steering, except that steering begins before the Rider spin stops. Phase II completes when the Rider stops spinning or when the Trikke steers past straight. If he stops spinning before passing straight, all of his Phase I angular momentum is transferred because spin and rotation are still alligned. However, there is less time to develop body spin for Phase II. If the Rider has delayed changing body spin beyond passing straight, there is no Phase I and nothing to transfer in Phase II.
Similar deductions about pre-steering plague the Contra technique. If the Rider stops spinning before passing straight, all of his Phase I angular momentum is transferred because spin and rotation are still opposed. The counter momentum built up will likely be less with less time to develop it, so there is less to make up for in Phase II. When waiting too long to start body spin nothing is available to transfer in Phase II.
Unlike the zero-sum exercise that the Contra Steering Technique is, Pre-Steering seems unadvisable for those desiring efficient locomotion.
The interpretive constraints of The Law of Conservation of Angular Momentum and the Parallel Axis Theorem lead to actionable Trikke Rider factoids. Separating out a working analysis frame of reference from a global one was key to negotiating the initial conditions needed to apply these constraints. These conclusions would be the same had no global frame been invoked and instead just started with a stationary Trikke at the beginning of each phase analysis. That would have seemed unsatisfying.
Once defined, four equations captured the dynamics of the technique phases. Each technique develops Rider angular momentum in Phase I that transfers to the Trikke-Glider in Phase II. No more angular momentum can be transferred in Phase II than is avaliable from Phase I. The only improvement to Phase I indicated in this process is to increase its duration by delaying steering. The Synchronous Steering Riding Technique prooved to be the best, perhaps enhanced by delayed steering. All of the Rider's Phase I angular momentum contributes to the Trikke's angular momentum and no more. Therefore, a Rider should keep Phase II to the shortest time possible if efficiency (less energy expenditure) is desired.
The equations developed above are further solved to provide some qualittaive results useful to developing computer models of Trikke riding. In particular, the Trikke-Glider corotation angular velocities given that of the Rider at the end of Phase I and Phase II.
Solve generally for ωt, the Trikke and Glider's co-rotation velocity around the turn center, in Equation 3 above. Orientation of ωr, the Rider's velocity, and value of the total angular momentum, Li, determine specific results.
Equation 7: Local Trikke-Glider angular velocity in terms of Rider spin
Equation 7 shows the general solution for local ωt in terms of ωr without regard to Phase initial conditions.
In the local frame at the beginning of Synchronous Phase I, Li = 0, ωr = 0, ωt = 0. The local frame rotates with the global angular velocity Ωt which can be positive (counterclockwise) or negative (clockwise). While the Trikke rolls out straight, ωr increases in a direction opposite to Ωt.
Equation 8: Body spin increases corotation in the other direction
Equation 8 shows that ωt and ωr must have opposite signs (all other symbols are positive). Increasing ωr in one direction, increases ωt in the other, the direction of Ωt. A reflection relationship.
As the Trikke turns out to straight, the distance to the turn center, R, increases to infinity. Nearing the limit where steering is straight, Equation 9 shows that Trikke-Glider corotation stops in the local frame:
Equation 9: local Trikke-Glider angular velocity is zero when steered straight
Optimally, the Rider's angular momentum reaches maximum when the front wheel points straight ahead. Equation 9 shows it has no effect on the local Trikke-Glider angular velocity, which is zero, when steered straight.
Beginning Synchronous Phase II, the Rider's spin aligns with the steering direction and is ideally at maximum Rider spin, ωrmax.
Equation 10: Local Trikke-Glider angular velocity during Synchronous Phase II
As the Rider slows his spin, the Trikke-Glider must increase in angular momentum acording to Equation 10. At the end Rider spin, ωr = 0 and ωt = ωrmax/Itg, in the same direction.
Analysis of Contra Steering works similar to that of these models. The variations don't change any of the basic results but they affect the interpretation of these models.
© Copyright 2023 Michael Lastufka