Body-Powered Trikke Physics

Trikke Levers and Mechanisms of Motion

Trikkes coast when not turning. To ride a Trikke is to constantly swivel the handlebars from one side to the other while coordinating the various activities that provide power to the system. Mechanisms that drive mechanical propulsion generally boil down to actions that move levers and push or pull rods. Levers, gears (which are notched, curved levers) and wheels all rotate. There are very few of these elements on a Trikke and fewer linkages between them. Some of the linkages identified are real. Others arise from real system components, like the road, in more conceptual ways.

Two primary types of actions, linear and rotational, propagate motion through mechanical systems. System analysts may describe these actions using "generalized coordinates" that guide forces and torques that shape and obey Equations of Motion, their dynamics and constraints. Solving these equations for energies, local accelerations, velocities, positions of parts, performance envelopes and global kinematics provide a deep understanding only visible in the details. This approach works best when the local dynamics lead seamlessly to global kinematics.

However, the simple mechanics of a Trikke provide formidable obstacles to such an approach, including being a nonholonomic system. Setting aside that machinery, this first principles study derives the local dynamics largely from momentum conservation. As the masses of Trikke components don't change significantly, the word "action" used below often means "momentum" or "velocity" rather than "energy" or "force" and "torque". The goal here is not to provide a global solution for the kinematics by solving equations of motion, but to elucidate the local dynamics that more scholarly approaches like [RoboTrikke] did not.

Organization: This report includes general terminology needed throughout, followed by an introduction of the moving-part "actors". Levers are illustrated and the mechanisms they animate are briefly described at an "executive" level. Physical concepts and some vector analysis required to understand and represent the mechanisms more precisely follow for the benefit of motivated readers. Conceptual derivations of the mechanism models provide the main body of the paper. Most of the interesting and useful insights are in these sections. I tried to make them accessible at some level to readers without a great amount of familiarity with physics or analysis. After conclusions, the appendices contain mathematical proofs, useful physical concepts and more detailed derivations of the physics models. The results of this analysis have been implemented in a forward-feed, discrete, [calibrated] Trikke/Rider [simulation] demonstrating typical Trikke [behaviors] that provide a basis for Trikke [magic].

Terms for Turning

Turns and words related to them form the context of Trikke motion; see the top view illustration in Figure 1. Turns are initiated by rotating the handlebars to the right or left around the steering column. The entire assembly that rotates and the casing that does not make up the stem (blue in diagram). Cambering the stem from side-to-side is not turning and does not result in a turn. It results from leaning the stem to the left or right.

The stem's wheel or guide-wheel (black object near top-left) touches the road on its contact patch, thought of as a point. "Guide" denotes best what the wheel does. Note, it is not a "drive" wheel; it's mainly passive, providing little forward impulse. This term distinguishes it from the trailing-wheels (other black objects) of the left and right arms.

The point around which the Trikke turns or orbits is its turn-center (black dot at bottom). When the Trikke turns left, it is to the left of the Trikke's forward axis (the x-axis along the center-line). Distance measured between the turn-center and a point on the Trikke is that point's turn-radius. A turn-radius is the length of the turn-ray from the turn-center pointing to the referenced point. To find the turn-center, locate the intersection of the line normal (black dashes) to the guide-wheel face at the contact point and the gray line between the trailing wheel contact points, the base-line. A Trikke traveling a straight line has an infinite turn-radius / turn-ray with undefined orientation. As a Trikke moves, its turn-center changes from moment-to-moment; it is instantaneous.

Inside the turn is toward the turn-center from the Trikke center-line, while outside is away from it. At a right angle to a turn-radius, pointing forward at a point on the Trikke is that point's path ray. It is always considered to be a unit vector; it has length 1. The purple ray near the top-left illustrates the guide-wheel contact point path ray.

Every model lives in some "domain". This one inhabits a 3-D mathematical world of local coordinates denoted by the basis vectors <X̑, Ŷ, Z̑>.

• x-axis, X̑: The forward direction of the Trikke is +x; parallel to the center-line
• y-axis, Ŷ: The left side is +y.
• z-axis: Z̑: Up is +z.

A turn to the left increases the steering angle θ (theta). Zero θ points straight ahead toward +x. Cambering the handlebars to the left decreases the camber angle γ (gamma) to negative values; its zero points straight up. These conventions maintain a right-handed coordinate frame when used with the usual vector operations.

Trikke Actors that Push and Pull

Conceptually, three assemblies, each with one wheel, coordinate the motion of a Trikke. They are controlled by a forth, the rider. Together these constitute the Trikke-Rider System (TRS). Two assemblies, the left and right arms, create a platform for the rider. They articulate with each other at the yoke via a cambering mechanism controlled by the third assembly, the stem. Moving the stem across the forward axis causes all three wheels to camber or lean from vertical in the direction of the stem. This action is called cambering. Two push/pull pairs of these assemblies implement the actors in the Trikke motive mechanisms.

In the analysis, some parts of the rider's body are considered to be part of the stem and the decks of the Trikke. For example, hands on the handlebars move with the handle bars, not the rider. Up to 15% of the rider's mass is considered part of the Trikke. This allows inertial effects to be modeled more accurately. In Figure 2 the rider-actor, lacking some mass, is dubbed the Reduced-Rider. Where the context is clear, any construct including the core of the rider is called "rider". The first combination analyzed below, includes most of the rider's body as one actor and the Extended-Trikke including the rest of the rider's mass as the other actor. A second partition of the system in Figure 3 isolates the the Extended-Stem that includes the steering column and forearms of the rider's body as one actor. The trailer includes most of the rider and everything else as the second actor.

Four Levers

Levers identified in mechanical systems are of three classes based on how their fulcrum, load and action are placed. "Linkages" connect their fulcrums, loads and actions. They can be physical levers minimally shaped like rods or irregular shapes bearing little resemblance to a rod without a line of material passing through its elements; in a sense "virtual".

One of the four levers involves the physical structure of the steering column with linkages extending from the guide-wheel's contact point to the handlebars. This Camber-Lever is a second-class lever with large mechanical advantage that makes moving the handlebars from side-to-side easy.

The most important lever is not physical in the same sense. Anchored at the instantaneous turn-center and extending to the guide-wheel contact point, the Turn-Lever "virtual" lever pulls the entire Trikke around. The physical linkages to the load of this lever are realized in the structure of the Trikke and extend to the road by the constraints of friction on all three wheels. It is also the longest lever, stretching almost to infinity.

Two more levers operate in tandem to rotate, pull and push the trailer into, toward and away from the guide-wheel contact. One is degenerate with action at the intersection of all three tubes, the yoke. This Yoke-Lever, has its fulcrum at the guide-wheel contact with load and action at the yoke. Its mate, the Trailer-Lever, extends from its action at the yoke, to the instantaneous transom point. Mostly, it rotates its load - the center of mass of the trailer.

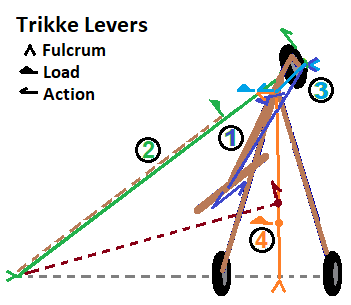
Figure 4 below illustrates the four Trikke levers. Movement of the dark brown dot, the TRS center of mass, is the goal of these levers. It is constrained to move in the direction of the dark brown ray. Along the way, the trailer's center of mass (orange dot) may also move.

1. Camber-Lever: As the rider steers and cambers a Trikke, the guide-wheel's contact point (green dot under guide-wheel in Figure 4) forms a fulcrum (blue ^) for the handlebar action (blue double-ray) through the Camber-Lever (blue line near circumscribed '1'). The yoke is the load (blue load). It is a second-class lever. Cambering can move the yoke side-to-side a couple decimeters. Because of the castered guide-wheel's negative rake, merely turning the stem also moves the yoke in orbit around the contact point. Yoke movement is the action behind "Castering" a Trikke. When the guide-wheel cambers, the rear-wheels camber with it to very near the same angle. They are permanently cambered about -5°; bottom further out than top.



2. Turn-Lever: Nothing happens in Trikke locomotion without involving this lever (green line near circumscribed '2'). When the stem is set to a particular turn angle, θ, lines (dashed-gray and solid-green) extended through each axle of the three wheels intersect at a point called the turn-center. As the name implies, a Trikke orbits this point at this turn-radius (green line), as long as the turn angle doesn't change. However, the turn angle constantly changes, so technically, the green line is the "instantaneous guide-wheel contact turn-ray". The turn-center is the fulcrum (green ^). Action occurs at the guide-wheel contact point (green patch under wheel with green ray). The TRS center of mass is the load acted on (displaced light brown dashed-line on the Turn-Lever). It can be a second or third-class lever.
3. Yoke-Lever: Extending from its stem contact fulcrum (light blue ^ under wheel) to the yoke, this degenerate lever (light blue line near circumscribed '3') rotates around the Camber-Lever. Due to the rotation, it acts (light blue ray) on the yoke, which is also its load (light blue load). It constitutes one of two levers involved with the castering mechanism.
4. Trailer-Lever: The trailer along with this lever (orange line near circumscribed '4') constitutes the second part of the castering mechanism. Action (orange ray) rotates, pushes and pulls this lever at the yoke. It is anchored at a transom fulcrum (orange ^) which causes it to move its load, the trailer's center of mass. It is a second-class lever and push-rod. The trailer includes the Trikke arms with their wheels and the rider minus body parts that are kinetically part of the handlebars - like hands and wrists. The trailer can be thought of as a distribution of sub-masses with two road contact points.

Three Mechanisms

Three mechanisms Jetting, Carving and Castering combine synergistically via the four levers to propel three-wheeled, body-powered Trikke riders' fun. Trikke locomotion is characterized by the serpentine track carved mostly side-to-side across a road as the rider coordinates steering, cambering and carving. These mechanisms allow riders to conjure the forces to snake out speeds over 4.5 meters per second on a level road. Note that "carving" includes "jetting", but jetting is the most fundamental mechanism of Trikke locomotion, so it is often mentioned outside of the carving context.

• Carving Mechanisms

  Jetting, Direct-Push and Direct-Pull are the carving mechanisms driven by two of the four Trikke levers. Jetting is the simplest, employing the virtual Turn-Lever. When activating any of these mechanisms, the rider produces an action at the guide-wheel contact point through rotation. The fulcrum of the Turn-Lever pivots on the turn-center causing the TRS center of mass, the load, to orbit the turn-center. Jetting pries the Turn-Lever like a crowbar dislodging a stone. Constrained to orbit and being solidly connected to the stem via human legs and metal bars, the TRS center of mass must move with the rotation of the lever.

  1. Jetting: This term comes from an old skiing technique used until the mid 1980's when ski materials improved dramatically. It involved shoving both feet forward to top small ridges or up-sloping turns. Dropping one's center of mass to power the jet made it difficult to maintain balance.

     Trikkes are much more stable and the jet is mainly performed one foot at a time - a hemijet. The physical goal of hemijetting (or just jetting) a Trikke is to accelerate the rotation of the outside arm around the Turn-Ray Lever into the guide-wheel path. When the guide-wheel accelerates, every part of the Trikke is compelled to accelerate with it in proportion to its turn-radius ratio. A part further from the turn-center than the stem orbits faster than the stem. The inside wheel orbits the slowest because it is closest to the turn-center. Model-wise, the guide-wheel pushes the Turn-Ray Lever which pulls the TRS center of mass around the turn-center. This is a consequence of the constraints provided by friction on the wheels.

     Unlike linear actions, jetting does not require the rider to "reset" center of mass position; the action is generated without moving the rider's local center of mass. There is NO recoil. When led by a hip twist and a delayed turn to the same side, the rider's angular momentum is first reflected then transferred to the Trikke-Rider pair as co-rotation via The Law of Conservation of Angular Momentum. Pure jetting is a ROTATION. Each of the other mechanisms describe how linear actions between Trikke components also synergistically feed into a jet rotation. A Trikke CANNOT move backward when the rider jets forward, unless slipping down a steep hill. A simple system that embodies momentum transfer through rotation is a turntable on a spinning platform.

     However, when turning to the left, jetting by rotating the left side of the body around to the front opposes the turn and reflects the jet into acceleration. The construction of the Trikke makes this difficult to perform from a stop so that a casual rider attempting it as an experiment does not experience much acceleration at all. Some riders may experience this differently and "wind up" before and during a turn, building bodily rotation but not releasing it to the Trikke, like caster does.

  2. Direct-Push and Pull

     Direct Push-Pull mechanisms feed into jetting, but lose some momentum in the process.

     1. Push: Assuming a Trikke is steered straight ahead, pushing it forward by recoiling the rider backward does not change the TRS center of mass location. The center of mass is stationary throughout the motion. However, the rider and Trikke centers of mass do shift position in opposite directions to conserve momentum.

        Constrained on an arch as a Trikke turns, the pushing rider and pushed Extended-Trikke agents generally have different turn-radii. When this is the case, conservation of angular momentum demands that a rider's push cause the TRS system center to move! However, the motion stops when the push stops. Never-the-less, the TRS center of mass takes a "step". During the step, a velocity manifests that is proportional to the ratio of the agents' moments of inertia and the ratio of Turn-Lever length to the TRS turn-radius. Motion ends as the rider and Extended-Trikke continue together as one unit in a perfectly inelastic collision. In the detailed derivation, this angular process is treated linearly via components at the guide-wheel contact point. Never-the-less, the Push orbital component becomes the jet and its radial component grounds into Earth's momentum via friction across the wheels. Angular and linear momentum are conserved.

     2. Pull: Pull is the opposite of Push. TRS center of mass location is stationary in a no-turn, linear pull. But like the direct-push constrained on an arch, the TRS center of mass is also not stationary. It takes a "step", but in the opposite (wrong) direction. Again, it originates from the conservation of angular momentum, while it ends in a perfectly inelastic collision. Opposite a push, a backward jetting rotation occurs via the Turn-Lever to motivate the step while the pull is in effect. The beauty of Trikke dynamics, one of many synergies, is that a push and turn to one side resets the rider's center of mass for a push and turn to the other side without needing a strong reset pull! It becomes a weak impulse, or better, no impulse.


• Caster Mechanism

  A couple of studies have concluded that a Trikke is propelled forward simply by cyclical steering; see [RoboTrikke] and [Roller Racer]. Personal experience shows this is a weak form of locomotion, especially starting from a stop. Note, it is very difficult to perform this task "pure castering" without throwing weight around or knowing for sure that the ground is level. Off you go when unintended jetting or downslope kicks in! When controlled to allow only castering (no cambering, extra jetting or slope) the guide-wheel contact point grinds in place. To emphasize caster-only locomotion, a rider must plant feet in front of the decks on the arm-bars close to the yoke. That moves the rider's center of mass forward enough to be demonstrably thrown into the turn by the Trailer-Lever; generating a decent jet. In normal practice, the rider is too far back to produce a caster-jet strong enough to initiate locomotion without added jetting or a good push. Furthermore, once moving, castering itself does not sustain speed, but crawls to a stop. However with wide, quick turns, direct-push and jet, castering weakly enhances a moving Trikke.

  3. Caster-Pull and Push

     1. Pull: When changing turn direction in a drive-cycle, the Yoke-Lever rotates the yoke pulling it closer to the guide-wheel contact point. Negative rake changes the guide-wheel contact point as the stem turns. When straight, the contact point is closest to the yoke and the yoke is highest above the wheel. As it turns outward, the contact point moves into the turn away from the descending yoke. The movement can be a few decimeters when cambering, especially sideways. Caster-Pull happens as the stem turns to the neutral, straight forward position.

        Pull occurs mostly sideways into the turn powered by the rider's handlebar twist and cambering. This causes a rotation of the Trailer-Lever. When the rider turns the stem very quickly, or moves forward on the deck platforms, turning resistance can be felt. Angular momentum around the transom point increases as the guide-wheel straightens and then passes on to the next stage of the mechanism - Caster-Push.

        Forward pull also occurs in this first half of the turn, but fizzles out as the guide-wheel absorbs it geometrically, merely by slowing its spin. However, the rise in yoke height above the wheel shrinks the base-projection distance to the transom causing the Trailer-Lever to shrink as much as one-percent. But this Direct-Pull is very small compared to the rotation and it dissolves completely when the wheel straightens. It is ignored in this Castering Model.

     2. Push: As the guide-wheel passes neutral (straight ahead), the Yoke-Lever lengthens due to negative rake as the contact point moves further into the turn and away from the yoke. This time, the wheel spins up covering the extra distance "shorting out" linear push-back on the yoke. Rotation increases the angular momentum of the trailer around the transom. Again, there is a change in Trailer-Lever length, but it is due to the drop in yoke height. It is too small to matter.

        When steering slows down near the end of the turn, the trailer's angular momentum releases as jet impulse in a perfectly inelastic collision until the turn stops. The strength of the impulse depends on how fast and how much the wheel is turned and the distance between the rider's center of mass and the yoke. The closer, the stronger. The jetting impulse produced during the end of the turn adds to the jetting rotation around the Turn-Lever that moves the TRS center of mass. Unlike the Direct Push-Pull mechanisms, castering does not result in a "step" and there is no "reset" needed. Like the Jet, it is a rotation.

Actions Constrained to an Arched Path

Wheels constrain a vehicle to travel a straight path or an arched path. Trikkes decelerate on straight paths, coasting to a stop. On a straight path, forward push accomplished by body recoil, does not move the TRS center of mass position under normal conditions. There is simply no sustainable way to accelerate a Trikke on a straight, flat path. Actions of the rider on an arched path, however, do propel the Trikke.

Each time a rider carves a Trikke away from its starting position, it tacks out a slightly different path, ending up in a different state. This nonholonomic behavior complicates the dynamics of the TRS. The normal development of equations of motion must be enhanced using constraints sustained by the three wheels via D'Alembert's principle. However, it is not necessary to develop complete equations of motion to derive useful quantities for understanding the TRS, but to leverage first principles and lots of diagrams.

The following dynamic motive models are based on momentum conservation. Pushing and pulling rely on the mechanics of linear momentum conserved as two masses separate or approach each other and then "rejoin" in an inelastic collision. This equal and opposite law also applies in angular actions. Rotation necessitates counter rotation. However, many of the counter reactions are synergistically consumed by constraints on the wheels grounding to the Earth's huge moment of inertia allowing only path-aligned actions to run free.

Rotation and Vectors

Vector and other various notations used in this study are described in Table 1 on the right. Distinctions among the different contexts in which vectors are commonly used have been made. For example, the free vector V̅ is decorated differently depending on whether it is being used as a position, bound as a ray, needed as a direction unit only or as a magnitude. Three dimensional vectors are used throughout.

Some aspects of rotation are purely geometric. For example, suppose a linear (aka. path, arch) velocity of a rotation is established at one point p͆ at radius r̚_p from its turn-center T͆_c. Then the path velocity of another point q͆ on the same rotating object is proportional to that at p͆ via v_ρp/v_ρq = r_p/r_q. Note, in the following "ρ" is used as a symbol indicating "path".

For objects constrained to motion on a path, a pattern that determines the amount of vector action imparted along a divergent path is most useful. The dot product gives the magnitude of the vector v̚ anchored at the path origin that aligns with the path ρ̑; a scalar. Multiplying by the path direction unit ρ̑ then gives the result u̚ as a ray with the direction of the path at the path origin. Note the parentheses in the following equation emphasize the order of operations. In many vector equations order does matter, but hints like parentheses may be omitted because there are other conventions at play.

Some vector patterns used in the derivation of the mathematical models of the physical dynamics of the Trikke are derived in Appendix A. For example, it is often necessary to solve a cross-product for one of its arguments. Cross Product Inverse shows one such derivation. Likewise, how to find the lever-arm of an action to a point of rotation is given in the Lever-Arm derivation. Vector Decomposition shows how lever-arms are important in deducing the motion of objects.

Some well known laws and theorems of Physics are also employed like Newton's Third Law and the Parallel Axis Theorem for moment of inertia.

Jetting Path Action Vectors

Gaining and maintaining top speed on a Trikke requires the mastery of alternate hemijetting (aka. jetting). A "jet" is the simplest and most direct motive mechanism of the three explored in this study. A rider generates a jet impulse in various ways involving the body core, legs and feet and/or shoulders and arms. Pinning the rider's center of mass to the inside of the turn and generating quick body rotation while thrusting a well placed foot on the outside of a turn does the trick. Subtle, well-coordinated arm, body tilting and slumping motions can increase effectiveness. However, upper body or lower body techniques can also be effective on their own. Alternating the techniques makes Trikking a total body fitness machine. Each motive mechanism feeds into the Jetting Model to produce locomotion. Jetting is the most basic motive mechanism of the Trikke and easiest to grasp.

Jetting as a Lever

Figure 5 illustrates the simplicity of "Jetting" to move the center of mass (purple dot) of a rotating system. Constrained to turn around its turn center (black dot) by its wheels, a Trikke rider initiates a rotation action (orange ray) by twisting and pushing into the guide-wheel path (brown arc). The entire Trikke-Rider System must turn at the same angular rate as the guide-wheel. Doing so, each part of the Trikke has a velocity at a right angle to its turn-ray, which originates at the turn-center. The distance between the turn-center and the part is its turn-radius. Divide the part's turn-radius by that of the guide-wheel's contact point to get its portion of the guide-wheel's speed. In the figure, the velocity of the Load (purple ray) is B/A times the speed of the guide-wheel contact, but at a right angle to the purple turn-ray. In this case, B/A is less than one, but when the guide-wheel turns in the other direction, B/A can be briefly greater than one.

Since angular momentum is always conserved, what rotates around the turn-center in the opposite direction of the rider's jet? Since the rider produced it, it's not the rider. Since the rider spins opposite to the turn before turning the other way, [Conservation] requires the Trikke-Rider system to co-rotate forward around the Turn-Center.

This "Magic lever" is a 2^nd class lever when B/A < 1 and becomes a 3^rd class lever when B/A > 1. It is also a virtual lever since there is no actual rod anchored at the ends of the turn-center and action. The road and its friction with the wheels create it. This paper does not consider how the action is created by the rider. Only that the rider has ginned up the action and overcome all the forces of nature to produce the velocity at the guide-wheel contact point. These include various types of friction and inertia. The rotational inertia of the system is best evaluated at the turn-center via application of the Parallel Axis Theorem to its parts. See Figure 14 for a jetting, carving demonstrator concept; perhaps not unlike what the [RoboTrikke] project attempted. Jetting is described in the context of Trikke dynamics in the next paragraphs.

Some of the local dynamic quantities have a local value and a global one. The local value represents the newly generated quantity during the infinitesimal time-span represented in the diagrams. Some of the local ones combine into their global counterparts. These global quantity symbols are not generally shown, but are understood to be there. For example, the TRS already moves with some global velocity v̚ at its position ©͆ in a snap-shot of time. The local value Δv̚ adds to that, becoming part of the global value. However, the local symbols are not generally prefixed with a 'Δ', since this study does not include equations in the global context except for the equations of motion.

Though the TRS does not turn freely around its center of mass, it is the best place to compute the local change in velocity. Its direction is known by constraint, its orbit. Only its magnitude remains, and that's dictated by geometry once the velocity of the guide-wheel contact point is known.

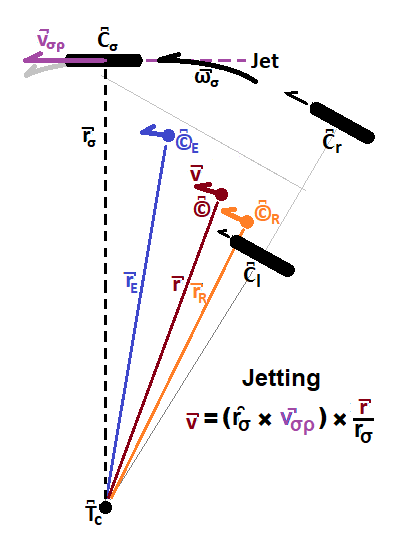
Two main actors appear in the Jet snap-shot diagram, Figure 6: the Extended-Trikke with center of mass at ©͆_E (blue dot) and the reduced rider with center of mass at ©͆_R (orange dot). In this section, "Trikke" means Extended-Trikke and "rider" means reduced rider. While purely jetting, the rider's position relative to the Trikke is stationary. Jetting is all about adding rotation ω̚_σ through the stem contact point C͆_σ (center of guide-wheel) around the turn-center T͆_c (black dot). The result of the rider's rotation action on the Trikke is linear motion v̚ (brown ray) along the TRS path unit ray ρ̑ (parallel to v̚). The effect of the input rotation ω̚_σ (thick black arrow) depends on the guide-wheel contact turn-radius r̚_σ (black dashes), and the specifics of the rider's technique that determines ©͆ and therefore r̚.

To avoid constructing a model of how the rider generates ω̚_σ (a future paper) consider the rider's jet input to be the locally generated linear velocity produced at the guide-wheel contact v̚_σρ (purple ray). From this linear velocity, the stem contact rotation ω̚_σ derives. All parts of the Trikke rotate around the turn-center at this angular velocity at the instant in time framed by the diagram. Its linear component at the TRS center of mass (brown dot) derives according to the simple geometry of the diagram. Note the Trikke's moment of inertia need not be accounted for by this use of v̚_σρ. Inertial resistance, the various wheel frictions and air resistance are assumed to have been overcome by the rider's effort in establishing this linear velocity.

Once ω̚_σ is known, the turn-ray from the TRS center of mass r̚ (thin brown line) factors into the velocity v̚ (thick brown ray) at the TRS center of mass ©͆ along the path ρ̑ (parallel to v̚). Like every part of the Trikke, ©͆ is constrained to move in orbit of the instantaneous turn-center T͆_c with rotation ω̚_σ due to the constraining power of the wheels at their contact points C͆_σ, C͆_l and C͆_r. The magnitude of v̚_σρ is simply related to v by r/r_σ.

Jetting can be reversed when a rotation ω̚_σ about the turn-center occurs in the opposite direction. The effects are clearly opposite those of a corresponding forward rotation. Though the "pulls" of the following mechanisms can produce such rotations, they are typically over-powered by the global rotation of the Trikke or nixed by the rider's technique. When there is an effect, it reduces the global rotation about the turn-center.

Summary of Derivation

The symbols involved in the Trikke hemijet model derivation are defined in Appendix B.

The purpose of this model is to find an equation for the locally generated instantaneous velocity of the TRS center of mass, v̚ due to rider jetting.

Given: The guide-wheel contact's linear velocity v̚_σρ generated by the reduced rider via jetting actions; The guide-wheel contact C͆_σ; TRS turn-center T͆_c; turn-rays for the guide-wheel contact r̚_σ and TRS center of mass r̚.

Find: The TRS velocity v̚ due to the rider's jetting rotation that results in a linear velocity of the guide-wheel contact path v̚_σρ.

Main lever-arm is C͆_σ - T͆_c.

The local instantaneous velocity of the TRS center of mass, v̚ derived for this Trikke hemijet model is:

eqn jp4: v̚ = (ȓ_σ × v̚_σρ) × r̚/r_σ

Pushing and Pulling a Trikke

As mentioned above, direct pushing and pulling on a vehicle traveling a straight line does little to promote acceleration. In some cases, a quick impulse can exceed natural frequency processes (as in starting a swing) or friction work functions (hopping a chair forward while seated) to cause system center of mass motion. Such were not found as sustainable mechanisms for riding a Trikke. These diagrams show that pushing and pulling a Trikke produce system acceleration moderated by the inertial properties and geometry of the actors. Computer model runs show that direct-push can contribute a significant momentum change in a carving cycle.

There are two actors (see Figure 2), the Extended-Trikke which moves at the guide-wheel contact point C͆_σ and the reduced rider with center of mass at ©͆_R. They are treated as semi-independent entities constrained to their arched paths and subject to the conservation of momentum. Combined, these produce a TRS center of mass displacement or "step". Analysis of this mechanism is almost as simple as jetting.

Linear vs. Angular Push/Pull

In terms of mathematical modeling, a Trikke's secondary mode of propulsion Direct-Push and Pull leverages the difference between linear and angular system center of mass motion; see Figure 7. When a linear push or pull is contained in a system, the center of mass of the system does not change (brown dots in left diagram). This is not so when the reaction of one actor (light blue dot in right diagram) is constrained to follow an arch. It also helps when their masses are quite different. The larger one (orange dot) gives more energy to the smaller one (light blue dot), which then travels farther on a circular path bending back toward the larger one on at least one axis (vertical axis in diagram).

In the linear push/pull diagram on the left, the system center of mass (brown dot) is not affected by the actions of the masses being pushed apart and then pulled together. The rays roughly indicate the direction and magnitude of the actions and the solid red and blue lines indicate the tracks of the masses. Conservation of momentum grants larger effects (action and track) to the smaller mass.

In the right diagram of angular push/pull inertial effects also favor the small mass. However, since the smaller actor must round the arc, it cannot be driven on an opposite path to the more massive body as in the linear case. Rather, it bends back forcing the system center of mass to leave its arc (indicated by green signed Δ) as it balances position between the two masses. Any deviation from its arc is an opportunity to drive other mechanisms. Note: an arc push on a Trikke can only contribute orbitally to the reaction, since radial reactions dissipate in friction and dump residual momentum to the Earth at right angles to the wheels.

Direct-Push Path Action Vectors

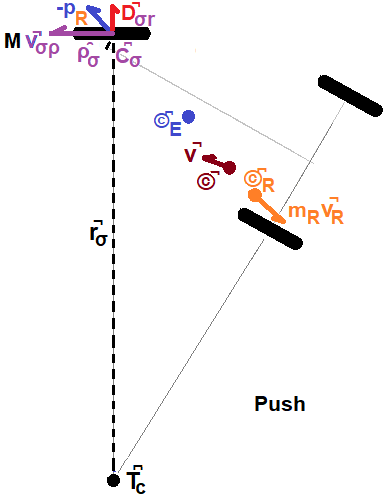
Movement of the rider generates a linear velocity v̚_R (orange ray in Figure 8). This produces a momentum proportional to the rider's mass m_R that must be balanced by the amount transferred via the guide-wheel path ρ̑_σ to the Trikke and rider plus that lost radially along ȓ_σ to friction and gained Earth momentum. Though it will ultimately move, ©͆_E (blue dot) is not the receiving focus of the rider's action. Rather, the guide-wheel contact point C͆_σ receives the separation action via a sequence of linkages during this snap-shot of time. Speed that would be imparted to ©͆_E manifests at C͆_σ because it is free to move, but it is constrained to align with its path direction unit vector, ρ̑_σ (parallel to v̚_σρ).

The force of the push acts equal and opposite to both the Extended-Trikke and rider - Newton's Third Law. However, the force is not typically aligned with the guide-wheel path. Therefore only its component aligned with the path (orbital) affects it, the rest (radial) becomes side-ways drag on the wheels. Stated in terms of momentum, before separation local momentum is zero. After the separation stops, the sum of momenta is still zero. But because the Extended-Trikke is constrained to movement in orbit around T͆_c (black dot), it can only receive angular momentum. The Rider is free to move anywhere during the separation. This means the two actors transfer equal and opposite angular momenta by conservation of that quantity, but the rider's linear - off orbit - momentum is dumped radially into friction at the wheels. This radial momentum causes the Earth to gain an opposite amount: first transferring some to molecules touching the wheels which alter physically, perhaps some chemically, and alter speed and rotation; secondly, any amount left over to the change the rotation of the Earth itself. Treating as a force or momentum transfer gives the same result when split into orbital and radial components.

This reasoning also shows that if the push (or pull) action v̚_R lies along ȓ_σ, no rotation is produced but the rider moves backward (or forward) at speed v_R with no effect on the TRS velocity. On the other extreme, when v̚_R aligns with the path ρ̑_σ, only rotation is produced which to first order has the same solution as the conservation of linear momentum with no movement of the TRS center of mass at all during the separation event. What happens between these extremes, is examined next.

When a force acts at an angle to a constrained path, it splits into perpendicular components, one along the path and one across the path. Their vector sum must add up to the original force. Such components are found by dotting the force vector by each path. In the push/pull analysis, the force along the path provides thrust for the orbital momentum while the force across the path increases the path-constraint drag at the wheel. For a real wheel, this sideways force may cause the wheel to slip to the outside of the turn on a push and to the inside on a pull. The model assumes no slip at all.

Finding the change in guide-wheel velocity due to a push or pull is straight-forward. See the result in the summary below.

The rider can only recoil backward so much before ©͆ travels behind the trailing wheel axles. At that point, the Trikke ride may end abruptly with a wheelie. Combined with the drive cycle time, this naturally limits how much push a rider can generate. In normal operation, the rider stops rearward movement to "join" the Extended-Trikke inelastically where the two bodies now behave as if stuck together. All the local momentum of the rider returns to the system stopping further ©͆ push-motion. What motion has occurred remains as a "step" in the displacement of the guide-wheel contact.

Direct-Pull Path Action Vectors

When the jetting action is reversed by a pull, the change in guide-wheel velocity also reverses. If the pull can be avoided, so can its displacement loss. When a turn and pull follows a push, the step achieved by the push is where the turn begins grabbing the pavement. The decelerating step of the pull can be "paid" for by the rider's jetting input. However, good riding techniques exist that avoid or greatly reduce a position "reset" pull due to the synergies of Trikke geometry.

Unconstrained, this mechanism converts pull into deceleration around the turn-radius of the guide-wheel which is the core of the jet mechanism. The Jetting input action is the increment in rear-ward linear velocity of rotation induced by the pull. ©͆_R and ©͆_E can only move until the rider ends the pull or bumps into the handlebars. They stop inelastically as the arms and legs of the rider hold m_R and m_E in place at the proximal extreme position. At that moment the masses "fuse", momentarily accelerating to the global TRS rotation.

Summary of Derivation

The symbols involved in the Trikke Direct Push-Pull Model derivation are defined in Appendix B.

The purpose of this model is to find an equation for the locally produced velocity of the guide-wheel contact point, v̚_σρ. This can then be used to determine TRS v̚ at ©͆ using the jetting model.

Given: TRS center of mass ©͆_R and previous ©͆_R' (used to determine the derivatives ∂(*)/∂t); guide-wheel path unit ρ̑_σ; rider mass m_R; guide-wheel contact C͆_σ; TRS mass M, orbit unit ρ̑_Trs and turn-center T͆_c.

Find: The TRS velocity v̚ via the intermediate linear velocity of the guide-wheel contact path v̚_σρ around T͆_c and the across wheel drag D̚ due to the push or pull.

Note when v̚_R · ρ̑_σ > 0, the rider is pushing into the guide-wheel path. When v̚_R · ρ̑_σ < 0, the rider is pulling.

Main lever-arm: C͆_σ - T͆_c

Jetting velocity input:

eqn dp6: v̚_ρσ = - m_R (∂©͆_R/∂t · ρ̑_σ) ρ̑_σ/(M ρ̑_Trs · ρ̑_σ)

This locally generated velocity is treated as input to the jet model to find its contribution to v̚ at the TRS center of mass.

The rider's recoil in terms of drag or friction at the wheels is

eqn dp7: D̚ = m_R ∂((∂©͆_R/∂t - (∂©͆_R/∂t · ρ̑_σ) ρ̑_σ)/(M ρ̑_Trs · ρ̑_σ))/∂t

Caster-Pull/Push Path Actions

So far, the motive mechanisms discussed are directly rider controlled. Castering is an indirect rider effort mediated by physical linkages from the guide-wheel contact point to the yoke, the Yoke-Lever and the Trailer-Lever. Computer model runs suggest caster-pull/push contributions at best attain about a seventh of the momentum that direct-push produces in a normal carving cycle. For the Trikke, it is a relatively complex, but small effect.

Caster-Pull is described first then Caster-Push, which is the mechanism with opposite x-axis orientation; both produce momentum primarily across the guide-wheel path. In a drive-cycle, the natural steering sequence invokes Caster-Pull followed by Push. A little jet action results as the Caster-Push transfers the Pull momentum from the trailer to the Trikke and rider. These actors are different from those involved in direct-push/pull. In castering, they are the Extended-Stem and Trailer of Figure 3.

Caster-Pull Action Vectors

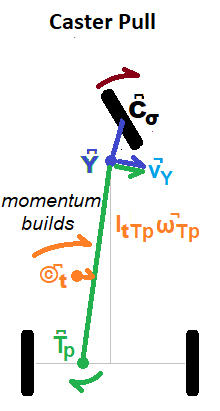
A turn toward the center (brown arrow in Figure 10) pulls the yoke Y͆ into the turn via the Yoke-Lever (blue line) and up to several centimeters closer to the contact point C͆_σ, especially with cambering. It also raises the yoke vertically up to five-centimeters. This in turn cranks the Trailer-Lever (green line) into the turn and brings it closer to the twisting guide-wheel contact point C͆_σ. This contraction mostly slows the guide-wheel rotation, but it also rotates the trailer's center of mass ©͆_t slightly into the turn and forward.

As the yoke rises, the trailer center of mass is drawn closer to the yoke by triangle geometry; the base decreases as the hypotenuse tips up; a Direct-Push. This contraction amounts to less than one-percent of the base-distance from yoke to transom T͆_p. It is ignored in this simple model.

What cannot be ignored is the yoke being pulled into the turn which causes the trailer to gain angular momentum around the transom. This momentum does not come from nor detract from the TRS. Driven by the rider, both the stem's local increase in angular momentum around the contact point and the trailer's are generated by turning the handlebars. Rotation of the Trailer-Lever (green arrow) moves the trailer's center of mass ©͆_t into the turn accounting for most of the momentum change. Note the trailer rotates around a point between the rear wheels closer to the one with greater instantaneous friction - the transom point. This angular momentum continues to build independent of the TRS until the stem turns past the forward direction and the turn slows.

Caster-Push Path Action Vectors

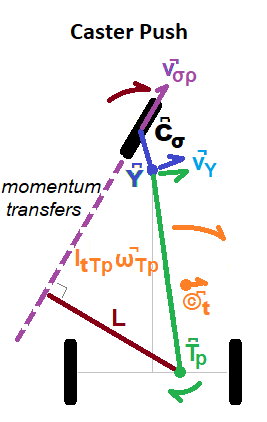
Continuing the turn past center, as illustrated in Figure 11, pushes the guide-wheel contact point C͆_σ and yoke Y͆ apart via the Yoke-Lever (blue line) and dips the yoke lower. The tire increases its spin. Especially when the tires have a tread pattern, the rider can hear the guide-wheel slow down with the pull, then speed up with the push. This action continues to crank the Trailer-Lever (green line) around the transom T͆_p and further into the turn, pushing it slightly backward as the yoke descends. This very slight Direct-Push is ignored in this model.

The trailer's angular momentum may continue to build as the trailer's center of mass ©͆_t continues to move. As the turn completes, the movement begins to slow down and its momentum is released through a jet (v̚_σρ) down the guide-wheel path in a perfectly inelastic collision. If the rider's center of mass approaches the handlebars, trailer momentum increases but the handlebars become more difficult to turn. When poised further back near the transom, trailer momentum contributes little, but turning is easy. The rider is also closer to and more aligned with the Trikke's minimum rotational inertia axis. Notice the lever-arm L in Figure 11. The longer it is, the more momentum feeds into the jet. When the wheel is straight, L has zero-length and no momentum is transferred. In summary, as the guide-wheel turns out, the lever-arm lengthens and momentum "bleeds" into the jet until the steering rotation stops.

Summary of Derivation

The symbols involved in the Trikke caster model derivation are defined in Appendix B.

The purpose of this model is to find equations for the contribution to guide-wheel contact point velocity due to Caster-Push. This velocity represents a jet that feeds into the Jetting Model.

Given: The wheel contacts C͆_σ, C͆_l, C͆_r, the absolute value of their path friction F_l, F_r and the center-line length; local yoke position Y͆; guide-wheel contact C͆_σ' C͆_σ", transom point T̑_p', its rotation ω̚_Tp' and time duration Δt' from the previous time-step; The guide-wheel path unit ρ̑_σ; TRS orbit unit ρ̑_Trs, mass M, trailer center of mass position ©͆_t, moment of inertia I_t, mass m_t and time duration Δt of the frame.

Find: The TRS velocity v̚ via the intermediate linear velocity of the guide-wheel contact path v̚_σρ using the Trailer-Lever rotation ω̚_Tp and angular momentum of the trailer around the transom point T͆_p.

Note when ∂C͆_σ(t)/∂t × T͆_p̑ - ω̚_Tp' > 0, the rider builds trailer rotation via turning toward or somewhat past straight. When negative, the trailer is transferring momentum to the TRS via the jet whose equation renders below.

Main lever-arms: C͆_σ - Y͆, Y͆ - T͆_p

Castering rotates the trailer around its transom point located in the local frame at:

eqn cp1 and cp2 combined: T͆_p = <-║center-line║, C͆_ly - (C͆_l - C͆_r)y F_r/(F_l + F_r), 0>

During the Caster-Push, the momentum from moving the yoke results in a jet velocity v̚_σρ.

eqn cp10: v̚_σρ = -(I_t + m_t (T̑_p - ©͆_t)²) ((T̑_p × (C͆_σ' - C͆_σ)/(T_p Δt)) - (T̑_p' × (C͆_σ" - C͆_σ')/(T_p' Δt'))) × (T͆_p - C͆_σ) × ρ̑_σ × ρ̑_σ/(M ρ̑_Trs · ρ̑_σ)

This locally generated velocity is treated as input to the jet model to find its contribution to v̚ at the TRS center of mass.

Conclusions

Adding angular momentum, jet, to a turning system predictably makes it turn faster! Utilizing a virtual lever to transduce that jet into system velocity makes riding a Trikke mysteriously magic for many. Direct push, typically a more intuitive mechanism, in a Trikke performs in a manner foreign to most people's experience producing cyclic steps or no effect at all. Rotation on a Platform helps illustrate wind-up in castering and jet and their subsequent release.

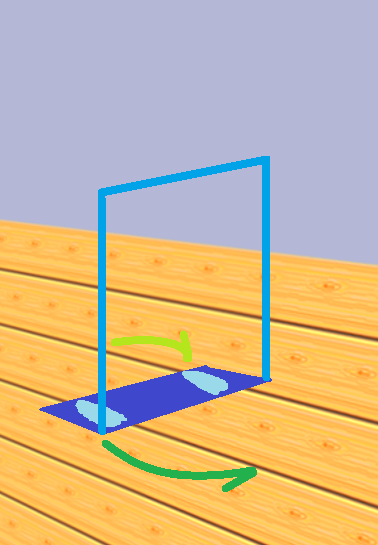
Stripping the TRS to first-order components and mechanisms exposes a simple toy many of us made as children when beckoned by a freshly waxed floor or new carpet. A piece of corrugated cardboard or carpet remnant (for the waxed floor) sufficed to slide across the floor. Inevitably, we began "walking" it across. Sliding it from side-to-side by rotating around the "planted" foot as much as possible. To this effect, hips swung to power the moving foot around. Then the other way around moving the other foot, each time shifting the weight to the planted foot. This is essentially a Trikke with no stem and no wheels, the Trikke arms reduced topologically to a rectangle of stiff, bottom-slick material as illustrated in Figure 13. As children, we instinctively understood alternate-hemijetting.

Conceptually, to add push and pull, anchor a light vertical frame to the slick rectangle. Shoving it forward and jetting a foot to separate the centers of mass (apparatus and child) causes it to slide. Suppose one kept balanced enough, the friction work function could be overcome to reset to the initial state without sliding back. Ready to push again. Though the behavior is similar to a Trikke, the reason the step is "kept" is not the same. The Trikke keeps it mainly because the rider can use the Trikke's geometry to avoid the pull.

Note this action is not skiing and it is subtly different from skating; it's "jetting"!

This look at Trikke physics does not include how the rider coordinates jet, push and caster. Each action must be coordinated and can be separately emphasized in rich and varied rides. An experienced rider can also produce a type of carving resonance. Quick cambering with the handlebars acts to restore the central stem position while jetting with both feet together to swing the trailer into the guide-wheel path against the stem's vertical rotational inertia. It is a tangible coordination between the two that feels like something children perform on a swing. Remember executing similar motions, hands grasping the chains while standing on a playground swing to achieve resonance against gravity? When quick enough, this type of resonance can help a rider maintain speed against the resistance of wind and slope or provide a fun, alternate way to ride.

Trikke Jetting Concept Demonstrators

Analyzing and modeling the dynamics of a mechanical system is often not enough to convince ourselves that the results are meaningful. Simulation data and graphics may seem realistic, but leave doubts about unknown or hidden flaws. Sometimes a physical demonstrator helps to bridge the credulity gap. In the spirit of [RoboTrikke], I offer these demonstrator concepts.

JettingBot

Jetting manifests when the rider's mass hovers on the inside of the turn near a trailing wheel and a rotation is produced into the guide-wheel path. Figure 14 presents a concept using a side-to-side swinging mass to produce both of those effects.

Note the familiar Trikke T-frame used in this paper's diagrams with two trailing wheels and a central spar (light blue). At the tip of the spar, a pair of limiters (purple) keep the guide-wheel from turning too far to the left and right. The caster-mounted wheel has negative rake so that it trails its pivot (orange dot) on the spar. It is free to turn up to the set limits. At mid spar, a pendular arm and weight pivots (orange shape) side-to-side. The larger dot at the back of the mass indicates it is much more massive than the small pivot in the front. Perhaps the motor and cam/gears can be part of this larger swinging mass. Success likely depends on the mass being greater than the rest of the demonstrator. No spring, limit switch, cam or gear design is offered here. That exercise is left to the reader. No batteries included. Your mileage may vary.

Operationally, the swinging mass accomplishes three goals. 1) It moves the center of mass closer to the inside trailing wheel of the turn. 2) The large mass causes the front wheel to turn to the same side when it abruptly stops. 3) While the mass swings across the frame, the frame's center of mass is pushed toward the inside of the turn continuing rotation into the guide-wheel path. Continuing, the mass reaches its oposite limit and rotation in the opposite direction to the current turn is produced. The entire system begins to rotate in the opposite direction. Each cycle, the guide-wheel turns the other way following the kick of the pendular arm and the center of mass moves into the turn due to angular acceleration of the mass-arm. When enough of the system's rotational inertia is engaged, the demonstrator should scoot along the guide-wheel's path in a zig-zag "carving" fashion. One digital robot configuration worked like this; it wasn't the best, but was simple.

RowBot

Figure 15 illustrates a sculling demonstrator concept that seems similar to carving. It's essentially a windshield wiper on wheels. In the rear over a pair of stabilizing wheels, a motor and gear box (black circle) produce the oscillating motion of the forward spar. At the tip of the spar, a pair of limiters (purple) keep the guide-wheel from turning too far to the left and right. The caster-mounted wheel has negative rake so that it trails its pivot (orange dot) on the spar. It is free to turn up to the set limits. The back-end must have more mass than the spar assembly to assure guide-wheel driven locomotion. This might be accomplished by housing batteries near the motor. The front wheel has to have enough weight on it to ensure traction.

In operation, the guide-wheel trails the side-ways motion of the spar, but only to the set limits. Setting the limits so the wheel turns almost perpendicular to the spar makes forward travel easier, but slower. This allows the push on the wheel to one side, but also guides some of that push into forward motion. This drive mechanism is fundamentally different than those of the Trikke. It simulates "sculling at the front of a boat" to pull forward.