| Lastufka Labs - | Reference |
Vehicles are made for motion. But they are only useful if that motion can be controlled. Control must be built-in to vehicles at design time and exercised during motion. Knowing how to build control into a vehicle and when to use it involves knowing what factors of motion can be controlled and what results to expect when they are changed. Modeling and experiments provide this knowledge.
Math and Physics come together in models of real-world systems. Not only can models help identify critical control and performance factors, but they can be used to determine the strength of various forces, speeds and friction coefficients after vehicular motion has been measured.
The model developed on this page is for powered motion. It can be applied to cars, boats, airplanes, rockets, bobsleds, trolleys, etc.. Though developed originally for small vehicles with reynold's numbers indicating smooth media flow (in air, water or both) with adjustments to calculate various driving forces, skin friction and incorporate various other types of interference friction, they can apply to "big" ones as well.
As with any model, there are assumptions made about the applicability of the model. These assumptions keep the model simple so it is more useful in practice. All models deviate from capturing REAL events to some extent. Some amount of error must be accepted because of this. This model attempts no characterization of motion deviating from a straight line of motion, though such motion is always present to some degree.
If the path of your real vehicle curves or oscillates measurably, an iterative computer model should be used. This model is mathematically minimal in the sense that there is a more complex one (derived somewhat differently) that will give the same "answers" (and deviations from reality) for more work. But, the more complex ones do not break down if the initial velocity is greater than the terminal velocity as this minimal model does. Fortunately, for this model, that will only happen if it is applied iteratively over small steps. It should be used only over "long" intervals.
Mathematical models use mathematical notation. The various environmental, structural and performance factors are written using short one or two letter symbols. Each factor also has physical units that relate to physical measurements that might be measured given appropriate instruments when possible. The table below presents the notations of the factors modeled.
| Symbol | Units | Description |
|---|---|---|
| F | oz | Force of propulsion along line of motion |
| M | ozs2/in | Inertial mass of vehicle |
| Df | oz | Sliding drag force on vehicle |
| k | ozs2/in2 | Media coefficient |
| v0 | in/s | Initial velocity |
| L | in | Length of powered run |
| t | s | Time of travel |
The various factors above are related to one another using physical laws and analysis. Some of these relationships have special meaning in understanding the model. These as well as kinematic factors (like time, acceleration, speed and distance) are recorded in the next table as a summary of the model.
| Description | Units | Expression |
|---|---|---|
| Equations of Motion | oz | Ma = F - Df - kv2 |
| Displacement Distance | in | Y = M/k |
| Initial Velocity | in/s | v0 = vc \[exp(-2(y-yc)/Y)-1] |
| Initial Velocity | in/s | v0(Ds=0) = v0'exp(-y/Y) |
| Momentum Transfer | ozs/in | P = \[k(F-Df)] |
| Displacement Time | s | T = M/P |
| Terminal Velocity | in/s | vt(F,Df) = \[(F-Df)/k] |
| Terminal Velocity | in/s | vt(y,t) = vt = Y arccosh(exp(y/Y))/t |
| Warm-up Time | s | t0 = T arctanh(v0/vt) |
| Warm-up Distance | in | y0 = - Y ln(\[1-v02/vt2]) |
| Time | s | t(y) = T arccosh(exp((y+y0)/Y)) - t0 |
| Velocity | in/s | v(y) = vt \[1-exp(-2(y+y0)/Y)] |
| Velocity | in/s | v(t) = vt tanh((t+t0)/T) |
| Distance | in | y(t) = Y ln(cosh((t+t0)/T)) - y0 |
| Acceleration | in/s2 | a(t) = Y/T2cosh2((t+t0)/T) |
| Driving Force | oz | F(k) = kvt2 + Df |
| Media coefficient | ozs2/in2 | k(F) = (F-Df)/vt2 |
Initial velocities are included for reference from their coasting models. If beginning from rest, the initial velocity is zero, v0 = 0.

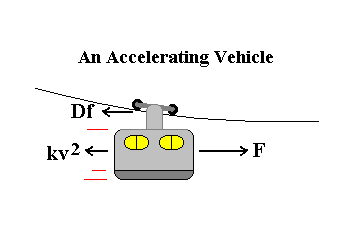
To model the acceleration of a vehicle we use a general form of Newton's second law, F = ma, that captures the forces that drive and oppose most vehicular motion,
Ma = F - Df - kv2
The inertial mass, M, for this general model must be coupled to acceleration along the line of motion. Wheels meet this criteria. Other parts like free spinning propellers may also. If there are no spinning parts, the mass of the vehicle is used for M. The inertial mass is a constant in the model, no mass is gained nor lost during travel. It may, however, be acceptable to allow some error due to mass change for something like a rocket that is much more massive than its propellant.
F is a constant driving force. It can be gravity, a steady stream of air, expanding gases, etc.. This force is often called thrust. The driving force is a constant in this model. Small changes in this force may be tolerated if using for example, the average force, leads to small acceptable errors in the model kinematics.
Df is a constant mechanical, sliding resistance. Generally, it is modeled as a scalar friction coefficient times a force that is at right angles to the sliding surface. It can be complicated by geometrical relationships to the surface on which the vehicle rests as with axle friction in wheels. This sliding friction is a constant in the model. In practice, this coefficient represents an average value since friction is, at this scale, essentially random.
All fluid media interactions that change in proportion to the speed of the vehicle squared, v2, are represented in the constant k. More than one media may be involved like air and water in the case of a boat. The terms expressing them are typically pressure drag terms (including lift) and skin friction terms. k is the effective mass of media moved aside per inch of motion, hence it is called the "media coefficient" here.
Since acceleration, a, is the change in speed over time, we can often find an expression for the speed over time. Separate out the time and speed dependencies noting that a = dv/dt; an acceleration is a small change in speed with respect to a small change in time. Divide through by the right hand side above, multiply through by dt and swap sides to get the two differential forms,
dt = Mdv/(F-Df-kv2)
These will be integrated below, but first it is useful to define some constants to make the expressions derived for this model more meaningful.
Given that the media coefficient, k, is the effective mass of fluid media displaced per inch of movement, dividing the inertial mass of the vehicle, M, by it gives a distance.
Y = M/k is the distance needed to move an air mass equal to the vehicle's inertial mass. This is the same with or without powered motion.
P = \[k(F-Df)] is the square root of the mass of media moved per inch of motion multiplied by the non-media forces on the vehicle. In terms of ROSI units, this is \[(ozs2/in2)oz] = ozs/in. ozs = (ozs2/in)(in/s) = mass times velocity = momentum. So P is the amount of momentum imparted by the vehicle to fluid media per inch of motion. It is called momentum transfer (per inch of motion) for this reason.
T = M/P is the inertial mass of the vehicle divided by the momentum transfer per inch of motion. Mass divided by momentum gives units of velocity. A distance divided by a velocity is a time. So, this displacement time, T, is the time needed to displace enough media mass to equal the vehicle's inertial mass at some speed.
We can use calculus to integrate the expression for small changes in time. The vehicle begins with an initial speed of v0, many times zero, while the clock starts at time zero. Any previous time can just be added to the time for powered motion modeled here since there are no explicit time dependencies. But speed determines aerodynamic resistance.
/ t / v | dt = M | dv/(F-Df-kv2) / 0 / v0
The large 'S' shaped symbols indicate a special kind of addition (called integration) over very small steps according to some rather complicated rules.
The result of evaluating these sums (by looking in a reference book; the easy part!) are the indefinite forms (in [..]s),
[t](0,t) = M [arctanh(v\[k/(F-Df)])/\[k(F-Df)]](v0,v)
where arctanh is the inverse of the hyperbolic tangent function. If you don't have a scientific calculator with hyperbolic functions, you can use this expression with the natural log function,
arctanh(x) = ln((1+x)/(1-x))/2
When the indefinite forms in the [..]s is expanded by evaluating at the limits in (,)s we get,
t-0 = M arctanh(v\[k/(F-Df)])/\[k(F-Df)] - M arctanh(v0\[k/(F-Df)])/\[k(F-Df)]
This says that the time spent accelerating from v0 to v is the time it would have taken to accelerate to v from rest minus the time it would have taken to accelerate to v0 from rest. Also, we will see that \[(F-Df)/k] is the terminal velocity, vt. Substituting the more meaningful symbols into the expression,
Let t0 = T arctanh(v0/vt) the time it would have taken to accelerate to v0 from rest. This is the "warm-up" time. Now we can write more clearly,
t(v) = T arctanh(v/vt) - t0
The argument of the arctanh function is a fraction that indicates how close to the terminal velocity v is. In an infinite amount of time, v reaches the terminal velocity where the argument becomes 1. The vehicle can not exceed the terminal velocity, vt, in this model.
Solve t = T arctanh(v/vt) - t0 to see how v changes with time.
We rearrange the expression as
arctanh(v/vt) = (t+t0)/T
and apply the hyperbolic tangent function to both sides to liberate v.
v/vt = tanh((t+t0)/T)
Multiply through by the terminal velocity to isolate v as a function of time.
v(t) = vt tanh((t+t0)/T)
The tanh function has a definition in terms of the exponential function,
tanh(u) = (exp(u)-exp(-u))/(exp(u)+exp(-u)) (for those of you like me whose scientific calculator has the exponential function, but not hyperbolic functions).
We can now truly recognize vt = \[(F-Df)/k] as the terminal velocity. The tanh function serves to "ramp" up to the terminal velocity over a period of time. Though your vehicle can get close to its top speed, it will theoretically never get there!
Terminal velocity is a special kind of matching velocity. To see this, square both sides of the definition and multiply through by k to get,
kvt2 = F-Df
This says that the force of media resistance is equally matched by the net force on the vehicle at the terminal velocity.
In practice, the expression for terminal velocity given above is not very useful unless you have made measurements of the driving force and friction forces. A more practical expression is worked out below that only requires a time and distance measurement.
We can continue the integration process realizing that the speed, v, is the change in position, y, with respect to time, v = dy/dt. It is fine to assume that the initial position is y = 0 and the initial time is t = 0 since whatever the real position and time are can just be added to the results we will get.
v = dy/dt = vt tanh((t+t0)/T)
The integral is,
/ y / t | dy = vt | tanh((t+t0)/T) dt / 0 / 0
The result of this integral is
[y](0,y) = vt [T ln(cosh((t+t0)/T))](0,t)
Evaluating at the limits gives,
y-0 = vtT ln(cosh((t+t0)/T)) - vtT ln(cosh(t0/T))
Again there is an extra term because of the distance it would have taken to get to speed v0, the "warm-up" distance.
Let y0 = vtT ln(cosh(t0/T)), it's the distance it would have taken to speed up to the initial speed, v0. By expanding t0, vt and T, y0 can be simplified,
y0 = \[(F-Df)/k]M ln(cosh((T arctanh(v0/vt))/T))/\[k(F-Df)]
A couple factors are inverses and cancel leaving,
y0 = Y ln(cosh(arctanh(v0/vt)))
This expression can be simplified even more, but we'll save that for later.
Similarly simplify the expression for y and use the y0 symbol to show that the distance traveled is the distance it would have taken to get to speed v minus the distance it would have taken to get to the initial speed.
y(t) = Y ln(cosh((t+t0)/T)) - y0
Solve for time, t, to get time in terms of the travel distance, y,
ln(cosh((t+t0)/T)) = (y+y0)/Y
Apply the inverse of ln, exp, and of cosh, arccosh, to both sides to get at the inner term with time, t, in it,
(t+t0)/T = arccosh(exp((y+y0)/Y))
Clear the constant from t by multiplying both sides by its inverse to finally get time, t, in terms of distance traveled, y,
t(y) = T arccosh(exp((y+y0)/Y)) - t0
Solve for a in the equations of motion to get the acceleration in terms of time,
a = F/M - Df/M - kv2/M
Make the time dependence clear by using functional notation getting ready to substitute for v(t).
a(t) = F/M - Df/M - kv(t)2/M
Substitute for v(t) using the notation for tanh squared, tanh2,
a(t) = F/M - Df/M - k(vt2 tanh2((t+t0)/T))/M
Dispose of extra parentheses and rearrange minimally to make the expression a bit easier to read before simplifying,
a(t) = (F-Df)/M - kvt2 tanh2((t+t0)/T)/M
Expand vt2 = (F-Df)/k to simplify to,
a(t) = (F-Df)/M - (F-Df) tanh2((t+t0)/T)/M
Distribute the 1/M and group to emphasize the common factors,
a(t) = (F-Df)(1 - tanh2((t+t0)/T))/M
Since 1 - tanh2(u) = 1/cosh2(u), we can write the simplest form for the acceleration,
a(t) = (F-Df)/Mcosh2((t+t0)/T)
But let's get this into a form more recognizable as an acceleration. Force is mass times acceleration, so multiply the right-hand-side by Mk/Mk,
a(t) = Mk(F-Df)/M2kcosh2((t+t0)/T)
Use the definitions of Y and P,
a(t) = YP2/M2cosh2((t+t0)/T)
Use the definition of T,
a(t) = Y/T2cosh2((t+t0)/T)
Y/T2 looks much more like an acceleration, in/s2, though (F-Df)/M is equivalent. cosh((t+t0)/T) goes to infinity as time does making the acceleration approach zero as terminal velocity is reached.
It is often useful to have the speed, v, as a function of distance, y,
v(y) = vt tanh((t(y)+t0)/T)
Expand the time expression,
v(y) = vt tanh(((T arccosh(exp((y+y0)/Y)) - t0)+t0)/T)
Some factors in the tanh argument are inverses and cancel out,
v(y) = vt tanh(arccosh(exp((y+y0)/Y)))
But we can do a lot better! By using the definition of a unit hyperbola,
1 = x2 - y2
and the relationship among hyperbolic trigonometric functions,
tanh(u) = sinh(u)/cosh(u) = y/x
we can write
tanh(arccosh(exp((y+y0)/Y))) = tanh(arccosh(x)) = tanh(u) where we have substituted x = exp((y+y0)/Y) and u = arccosh(x)
Since tanh(u) = y/x all that needs to be done is to solve for y in terms of x, plug this new expression for tanh(u) in terms of x in the expression for v0, expand x and simplify.
y = \[x2-1]
Substitute y into the expression for tanh(u) where we left off two lines above,
tanh(u) = y/x = \[x2-1]/x = \[(x2-1)/x2] = \[1-1/x2]
Expand x,
tanh(u) = \[1-1/exp(2(y+y0)/Y)] = \[1-exp(-2(y+y0)/Y)]
Substitute this into the expression for v(y) to get,
v(y) = vt tanh(arccosh(exp((y+y0)/Y))) = vt \[1-exp(-2(y+y0)/Y)]
It's like collapsing a telescope. This is a much easier expression to work with.
The distance it would have taken to get to the initial speed with the constant force pushing the vehicle, y0, can be simplified further.
y0 = Y ln(cosh(arctanh(v0/vt)))
By using the definition of a unit hyperbola again,
1 = x2 - y2
and the relationship among hyperbolic trigonometric functions,
tanh(u) = sinh(u)/cosh(u) = y/x implies arctanh(y/x) = u
we can write
cosh(arctanh(v0/vt)) = cosh(arctanh(v0/vt)) = cosh(u) where we have substituted y/x = v0/vt and u = arctanh(y/x)
Since cosh(u) = x/\[x2-y2], we can factor y out of the denominator to get,
cosh(u) = (x/y)/\[(x/y)2-1]
Plug in the value of x/y (= vt/v0) to get a new expression for cosh(u).
cosh(u) = (vt/v0)/\[vt2/v02-1]
Distribute the v02 factor to get,
cosh(u) = vt/\[v02(vt2/v02-1)] = vt/\[vt2-v02] = 1/\[1-v02/vt2]
Substitute this into the expression for y0 and invert the natural log argument to get a minus sign out front,
y0 = - Y ln(\[1-v02/vt2])
Start with terminal velocity,
vt = \[(F-Df)/k]
Solve for driving force, F,
F(k) = kvt2+Df
To get the coefficient, k, start over with terminal velocity,
vt = \[(F-Df)/k]
Solve for it,
k(F) = (F-Df)/vt2
The long form of F(k) that will be useful to get an expression of terminal velocity in terms of distance and time is obtained via t(y) with v0 = 0 (y0 = t0 = 0),
t(y) = M arccosh(exp(y/Y))/\[k(F-Df)] with T expanded
Multiply by denominator and square,
k(F-Df)t2 = M2 arccosh2(exp(y/Y))
Divide out the time and add the drag to both sides,
F(k) = M2 arccosh2(exp(y/Y))/kt2 + Df
Using the longer expression for driving force a mathemagical feat can be performed so you can find out the terminal velocity of your vehicle knowing at least one measurement of time and distance. Armed with the terminal speed, you can find your vehicle's speed profile along its entire path without knowing the driving force nor the sliding friction!
Start with the expression for terminal velocity from above getting ready to substitute in the long expression for driving force, F.
vt = \[(F-Df)/k]
Plug the driving force in,
vt = \[((M2 arccosh2(exp(y/Y))/kt2 + Df)-Df)/k]
The drag terms cancel,
vt = \[M2 arccosh2(exp(y/Y))/k2t2]
Everything in the squareroot is squared so remove it,
vt = Y arccosh(exp(y/Y))/t
Though this expression makes it EASY to measure your vehicle's potential for speed, you need to use the result in the expression for velocity in terms of distance, v(y) to find your vehicle's actual speed.
| [Back] | [Central Console] |
| Lastufka Labs - | Reference |
| Copyright © 1998, 2002 by Michael Lastufka, All rights reserved worldwide. | |